4

Farmer Brown is standing in the middle of his perfectly circular field feeling very content. It is midnight and there is no moon and unknown to the farmer, Martian zoologists are landing randomly at points on the circumference of his field. They land at one minute intervals, starting at midnight. As soon as there are martians at points A,B,C such that triangle ABC contains the center of the field, Farmer Brown will be teleported to the waiting space-ship and transported off to spend the rest of his life as an exhibit in a Martian zoo. What is the expected time until he is abducted?

My approach:

If lets say the farmer gets abducted after k Martians land. This implies that the first k-1 martians all lie in the same semicircle. Also, the kth martian lies on the circle such that the far away martians in the initial k-1 martians, and the kth martian form a triangle that contains the center of the circle.

The probability that the first (k-1) martians don't contain the center of the circle is

formo

(see here). Also, the probability that the kth martian makes the center lie in a triangle formed by the kth martian and the ends of initial k-1 martians should be 1/4, since this is equivalent to the situation of only 3 martians.

So the expected value of k, i.e. no. of martians after which the farmer gets abducted, should be
form

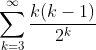
The answer I get from this, is 3.5. Whereas the actual answer is 5. In the solution in that link, I don't understand where does the right hand side of the probability equation come from. Where is my approach wrong?

Christian Blatter
  • 232,144
qwerty_uiop
  • 321
  • That's equivalent to the question of probability that n points chosen randomly on the circumference of a circle lie within the same semicircle or not. – qwerty_uiop Nov 03 '18 at 16:51
  • “...since this is equivalent to the situation of 3 martians”: no, it’s not. The distance between the two extreme martians is not distributed the same as the distance between the first two martians. If this is not obvious to you, let me know, and I will try to clarify. – TonyK Nov 03 '18 at 19:46

1 Answers1

2

So you know that the probability that $k-1$ martians do not hold the farmer is $$G(k-1)=\frac{k-1}{2^{k-2}}$$ Then the probability that $k$ martians do not hold the farmer is $$G(k)=\frac{k}{2^{k-1}}$$ and the probability that the $k$-th martian catches the farmer is $$P(k)=G(k-1)-G(k)=\frac{k-2}{2^{k-1}}$$

Finally $$E[K]=\sum_{k=3}^{\infty}k\frac{k-2}{2^{k-1}}=5$$

kludg
  • 2,667
  • Right, makes sense. So I am making a mistake in assuming that when I add the kth martian, P(k) = G(k-1) * 1/4. I'm not yet sure why is this incorrect. – qwerty_uiop Nov 03 '18 at 16:43