2

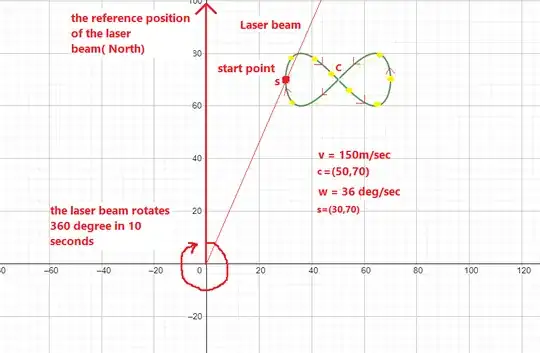
There is a body moves along an eight figure path and there is a laser beam at the origin that rotating with rotation rate $w$.
How to get the points that originate each rotation from the intersection between the moving body path (eight figure) and the rotating beam.

Note that the laser beam is used for nothing but only as time reference.

Given:

  1. the equation that describes that path:
    $(x-h)^4 = a^2((x-h)^2-(y-k)^2)$
    where $(h,k)$ = (50,70)

  2. The start point of the curve $(X_S,Y_S)$
    where $(X_S,Y_S)$ = (30,70).

  3. The speed of the moving body ($V$=150 m/s).

  4. The speed of rotation of the laser beam $w= 36$ deg/sec.

  5. The value of a = 10.

Required:

The points on the curve that came from the intersection between the beam line and the motion path (yellow points on the attached figure).

Please note that:
I do not know any information about how many points came from the intersection between the body path and the beam, for sure it depends on the body speed and the rotation rate of the beam.

Here is a figure for more illustration:

enter image description here

AAEM
  • 190
  • You wrote, "How to get the points that originate each rotation from the intersection between the moving body path (eight figure) and the rotating beam." I can't understand this sentence. Could you please rephrase? – Adrian Keister Sep 18 '18 at 17:13
  • 1
    @AdrianKeister when the moving beam start to rotate, it will hit the body which moves in an eight figure path, i want to get the points of hits(between the line and the body) or in other words (the points of intersection between the beam and the path of the body(eight figure)). those points will appear every rotation because the beam hit the body once per complete rotation – AAEM Sep 18 '18 at 17:16
  • 1
    Does the beam hit the body at point $(X_S,Y_S)$ initially (i.e., at time $t=0$)? Are we given the value of $a$? – Batominovski Sep 18 '18 at 17:23
  • @Batominovski the beam start to rotate initially from the north but its first hit with target at s, and the value of a =30 – AAEM Sep 18 '18 at 17:33
  • 2
    Let $\big(r(t),\theta(t)\big)$ denote the polar coordinates of the particle at time $t$. Thus, the laser hits the particle at time $t$ if and only if $$\theta(t)\equiv wt+\phi_0\pmod{2\pi},,$$ where $\phi_0$ is the initial phase of the laser (namely, the laser's direction at time $t$ is given by the equation $\phi(t)=w t+\phi_0$). From your description, $\phi_0=\dfrac{\pi}{2}$. Thus, you will need to solve for $\theta(t)$, which does not look very fun. – Batominovski Sep 18 '18 at 17:34
  • You could parametrize the figure eight, and use $\theta(t)=\arctan(y(t)/x(t)),$ which works because everything's in the first quadrant. Pick a $t$, compute $x$ and $y$, then get $\theta$. – Adrian Keister Sep 18 '18 at 17:37
  • 1
    And I would expect that there are finitely many intercepts if and only if the period $T_l:=\dfrac{2\pi}{w}$ of the laser beam's rotation, and the period $T_p:=\dfrac{L}{V}$ of the particle in the figure-eight path satisfy $\dfrac{T_p}{T_l}\in\mathbb{Q}$. Here, $L$ is the arc length of the figure-eight curve (which looks very ugly, i.e., $L\approx 6.09722,a$, so I expect infinitely many intercepts). However, I do not have the will power to try to solve for $T_p$ exactly, or to find out what the intercepts are. – Batominovski Sep 18 '18 at 17:41
  • @Batominovski make it more simpler and i will give it a try – AAEM Sep 18 '18 at 18:09
  • What is the "it" that I should make simpler? – Batominovski Sep 18 '18 at 18:17
  • @Batominovski ok, what do you mean by $(mod2π)$, also you said that "you will need to solve for $θ(t)$, which does not look very fun", i do not know why should i solve for $θ(t)$? – AAEM Sep 18 '18 at 18:30
  • It means that $$\theta(t)-wt-\phi_0=2n\pi\tag{*}$$ for some integer $n$. And you are going to need to get the value of $\theta(t)$ if you want to solve Equation (*). – Batominovski Sep 18 '18 at 18:31
  • @Batominovski in the Equation ; $w$ is the rotation of the beam what about the value of $t$ in Equation ? do we know the time at which the hit happens? – AAEM Sep 18 '18 at 18:38
  • You are solving (*) for $t$. So, no, a priori, you don't know $t$. You can determine a general expression for $\theta(t)$ in order to solve (*), even if it is probably very ugly. – Batominovski Sep 18 '18 at 18:39
  • @Batominovski now i get confused, you said that " you are going to need to get the value of θ(t) if you want to solve Equation ()" and here you say that we are going to solve for t, so how can i get the values of θ(t) ? – AAEM Sep 18 '18 at 18:42
  • No, you can get $\theta(t)$ for a *general* value of $t$. But you want to solve (*) for a *specific* time $t$ at which the laser intercepts the particle. – Batominovski Sep 18 '18 at 18:43
  • Like, I can determine the value of the function $f(x)=x^2-2x-3$ at any *general value* $x$ (that is, you give me the value of $x$, and then I can tell you what $f(x)$ is), but if I want to find the root of $f(x)$, then I need to solve for a *specific value* of $x$ such that $f(x)=0$ (namely, $x=-1$ and $x=3$). – Batominovski Sep 18 '18 at 18:45
  • @Batominovski could you please solve for the first intersection and i will make the extra intersections, i would be very thankful – AAEM Sep 18 '18 at 18:58
  • Unfortunately, no. While you can get find $\theta(t)$ for a general time $t$, it is a very tedious job, and I am not willing to spend that much time dealing with it. – Batominovski Sep 18 '18 at 19:01
  • 1
    How is this substantially different from your previous (and more general) question? – amd Sep 18 '18 at 23:58

1 Answers1

1

I haven't solved the question, but I have an approach you can try.

You have the starting point and the speed and the curve. So you should be able to get the position of the body as a function of time.

Solve speed = 150 m/s = $ \sqrt{ \frac{dx}{dt}^2 + \frac{dy}{dt}^2 }$ and $ 4(x-h)^3 \frac{dx}{dt} = a^2[ 2(x-h)\frac{dx}{dt} - 2(y-k)\frac{dy}{dt}] $

to get $\frac{dx}{dt}$ and $\frac{dy}{dt}$. You also have the initial position $(x_0,y_0)$.

So now you have the position of the body as a function of time as $x = x_0 + \int x(t)$ and $y = y_0 + \int y(t)$.

For the next part, try converting to polar coordinates by using $x = r cos \theta$ and $y = r sin \theta $.
This way, you will have the angle the position vector of the object makes with the x-axis at the origin as a function of time.
Equate that to the laser's angle and you get your theta values. This can further give you the times and therefore the position of the body.

Hope this helps.

AAEM
  • 190
MathNerd2017
  • 61
  • it would be better to provide complete answer – AAEM Sep 30 '18 at 10:12
  • The complete answer would require a lot of calculation, which would require time. Also, you haven't given the value of 'a' in the equation of the path. Check out this link to work with this kind of paths. – MathNerd2017 Oct 01 '18 at 01:35
  • I will try to solve but i need to know the following : (1)what do you mean by "to get dx/dt and dx/dt" i think it is a typo? (2) after simplifying the equation to be function only in {x,y and (dy/dt)}, how can i calculate dy/dt? (3) what is x(t) and y(t) represent for? (4) how can your approach substitute for the antenna rotation (Omega)? – AAEM Oct 01 '18 at 10:26
  • Yes, it is. Sorry about that.
    • – MathNerd2017 Oct 01 '18 at 17:02
  • The resulting differential equation is time consuming to solve. I'm not exactly sure how to solve the one that you get. 3) They are the x and y co-ordinates of the body i.e. the position of the body as a function of time from the starting time when the initial position is given.4) Once you have the position as a function of time, you can simply use $\theta = tan^{-1} \frac{y(t)}{x(t)} $ to get the angle subtended at the origin as a function of time. You already know the laser beam's angle as a function of time $ \theta = 36t$. So equating both will give you the intersection points.
    • – MathNerd2017 Oct 01 '18 at 17:13
  • the differential equation is function in 3 unknowns, so how can i try to solve? – AAEM Oct 02 '18 at 08:18
  • There is a relation between $x$ and $y$ ( the path of the object) so the differential equation will be in terms of $\frac{dx}{dt}$,$x$ and $t$ for $x(t)$ and similarly for $y(t)$. – MathNerd2017 Oct 02 '18 at 18:02