Is the limit of this infinite step construction an equilateral triangle?

Question

Just for fun (inspired by sub-problem described and answered here):

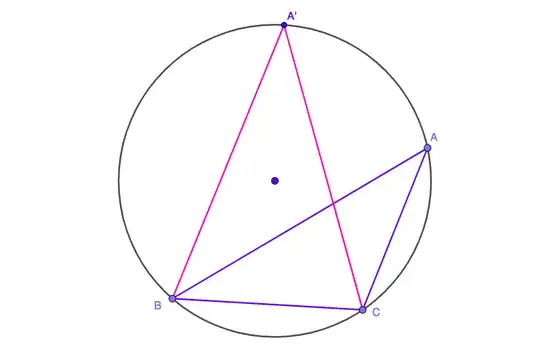
Let's pick three points on a circle, say $A,B,C$. Move one point ($A$ for example) until the triangle becomes isosceles ($A'BC$) with all angles acute:

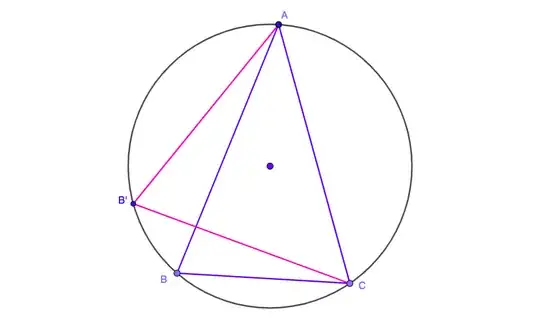
Now we have triangle with sides $AB$ and $AC$ equal. Pick any of the two, say $AC$ and move $B$ until the triangle becomes isosceles again, with all angles acute:

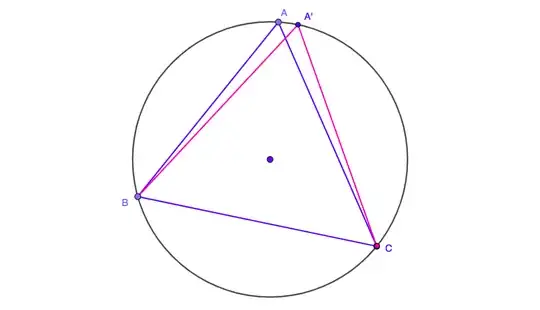
Now we have a triangle with sides $AB$ and $BC$ equal. Pick any of the two, say $BC$ and move $A$ until the triangle becomes isosceles again, with all angles acute:

Repeate the same process infinite number of times.

Can we prove that the end result is always an equilateral triangle? It looks so but I might be wrong. I have checked several initial configurations and always ended up with something looking like an equilateral triangle.

Answer 1

Think about what happens to the maximum difference between angles over time.

For simplicity, let's start with an isoceles triangle with angles $x,y,y$. This triangle has "maximum angle difference" $\vert y-x\vert$. Then when we move one of the $y$-angled points, our new triangle will have angles

$$y, {x+y\over 2}, {x+y\over 2}$$

since the angle of the point being moved doesn't change.The maximum difference of angles in this new triangle is

$$\left\vert {y\over 2}-{x\over 2}\right\vert={1\over 2}\vert y-x\vert.$$

So each time we perform this transformation, the maximum angle difference goes down by a factor of two. Whatever the initial value $\vert y-x\vert$ was, this means that the maximum angle difference goes to zero,$^*$ which in turn means that in the limit the angles are equal.

---

$^*$This is because it's a geometric sequence with ratio in $(-1,1)$ (namely, ${1\over 2}$): if $r\in(-1,1)$ then for any $a$ we have

$$\lim_{n\rightarrow\infty}ar^n=0.$$

Note that it would not have been enough to simply know that the maximum angle difference decreases, since not every decreasing sequence goes to zero!

Answer 2

By the Inscribed Angle Theorem, moving a vertex around the circle preserves the angle at that vertex. Now, suppose that, at stage $i$, the apex angle is $\theta_i$, so that the base angles are $\frac12(\pi - \theta_i)$. But this apex angle was the base angle of the previous step, giving this recurrence $\theta_{i} = \frac12(\pi-\theta_{i-1})$. Thus, $$\begin{align}\theta_n &= -\frac12\theta_{n-1} + \frac12\pi \\[6pt] &=\frac12\left(-\frac12(\pi-\theta_{n-2})+\pi\right) = \frac14\theta_{n-2}+\frac12\pi-\frac14\pi \\[6pt] &= \cdots \\[6pt] &= \left(-\frac12\right)^{n}\theta_0 \;-\; \sum_{i=1}^n\left(-\frac12\right)^{n}\pi \\[6pt] \lim_{n\to\infty}\theta_n &= 0\cdot\theta_0 \;-\; \frac{(-1/2)}{1-(-1/2)}\pi \\ &=\frac{\pi}{3} \end{align}$$

Thus, in the limit, the triangle becomes equilateral. $\square$

Answer 3

Assume WLOG that the initial triangle is isoceles. Let $\alpha$ be the apical angle, and let $\beta$ be a remaining angle. Then the transformation in question sends

$$\begin{bmatrix}\alpha \\ \beta \end{bmatrix}\mapsto \begin{bmatrix}0 & 1 \\ \tfrac{1}{2} & \tfrac{1}{2} \end{bmatrix} \begin{bmatrix}\alpha \\ \beta \end{bmatrix}\text{.}$$ Let $\mathsf{X}$ be the $2\times 2$ transformation matrix on the rhs. $\mathsf{X}$ has characteristic polynomial $x^2-\tfrac{1}{2}x-\tfrac{1}{2}=0.$ By the Cayley–Hamilton theorem, $$\mathsf{X}^2=\tfrac{1}{2}\mathsf{X}+\tfrac{1}{2}\text{.}$$ Therefore we have a Sylvester formula $$f(\mathsf{X})=f(1)\left(\frac{1+2\mathsf{X}}{3}\right)+f(-\tfrac{1}{2})\left(\frac{2-2\mathsf{X}}{3}\right)$$ for any polynomial $f$ (where the matrices in brackets are the Frobenius covariants). Thus, $$\mathsf{X}^n=\frac{1+2\mathsf{X}}{3}+(-\tfrac{1}{2})^n\left(\frac{2-2\mathsf{X}}{3}\right)\text{.}$$ The second term converges to zero, so $$\begin{split} \lim_{n\to\infty}\mathsf{X}^n&=\frac{1+2\mathsf{X}}{3}\\ &=\frac{1}{3}\begin{bmatrix}1 & 2 \\ 1 & 2\end{bmatrix}\\ &=\frac{1}{3}\begin{bmatrix} 1\\ 1\end{bmatrix}\begin{bmatrix}1&2\end{bmatrix}\text{,} \end{split}$$ $$\lim_{n\to\infty} \begin{bmatrix}0 & 1 \\ \tfrac{1}{2} & \tfrac{1}{2} \end{bmatrix}^n \begin{bmatrix}\alpha \\ \beta \end{bmatrix}=\begin{bmatrix}\tfrac{\alpha+2\beta}{3}\\ \tfrac{\alpha+2\beta}{3}\end{bmatrix}\text{.}$$ i.e., the apical and side angles approach equality as the operation is repeated.