Permutation of points $P_i\in X$ such that $\sum^n_{j=1}|P_{\sigma(j+1)}-P_{\sigma(j)}|^2\leq 8$

Question

I am dealing with the test of the OBM (Brasilian Math Olimpyad), University level, 2017, phase 2.

As I've said at others topics (questions 1 and 2, this last yet open, here), I hope someone can help me to discuss this test.

The question 3 says:

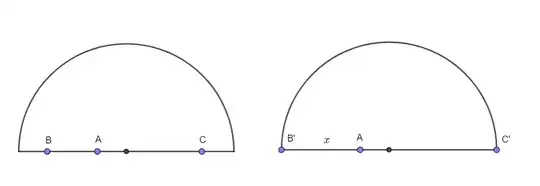
Let be $X=\{(x,y)\in\mathbb{R}^2|y\geq 0, x^2+y^2=1\}\cup \{(x,0),-1\leq x \leq 1\}$ the border of a semi-disc closed with radius $1$.

a) Let be $n>1$ an integer and $P_1,P_2,...,P_n\in X$. Prove that exists a permutation $\sigma:\{1,2,...,n\}\rightarrow\{1,2,...,n\}$ such that $\sum^n_{j=1}|P_{\sigma(j+1)}-P_{\sigma(j)}|^2\leq 8$

where we define $\sigma(n+1)=\sigma(1)$.

b) Determine the sets $\{P_1,P_2,...,P_n\}\subset X$ such that for all permutation $\sigma:\{1,2,...,n\}\rightarrow\{1,2,...,n\}$ ,

$\sum^n_{j=1}|P_{\sigma(j+1)}-P_{\sigma(j)}|^2\geq 8$

where we define $\sigma(n+1)=\sigma(1)$.

Well. I draft the solution as following:

We'll show that the permutation such that $P_{\sigma(1)}P_{\sigma(2)}...P_{\sigma(n)}$ is a convex polygon respect the inequality.

We'll call $\sigma_n$ one of these permutations to $\{P_1,P_2,...,P_n\}$ and define $S_n=\sum^n_{j=1}|P_{\sigma(j+1)}-P_{\sigma(j)}|^2$.

These notations will help us in our proof by induction.

So:

1) The case $n=2$ (trivial)

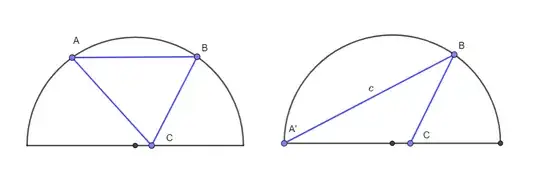
2) The case $n=3$ is my problem

3) To indution, I used the following result:

All of the convex polygon with more than $3$ sides have at least one internal angle $\geq 90^o$ (the inequality is strict to $n>4$)

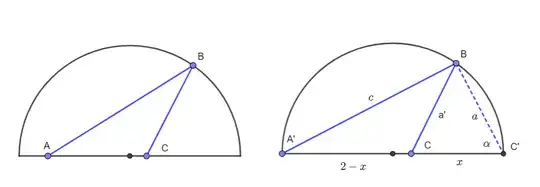
I've proved this result and I've combined it with the fact that the on a triangle with sides $a,b,c$ such that the angle between $a$ and $b$ is $\geq 90^o$, we have $a^2+b^2\leq c^2$.

I've wrote a long proof trying combine these results and it's a little dificulty to me write it here today, but if someone want, I can try.

Well, as I've said, my problem is with $n=3$, particularly, acutangles triangles enrolled on $X$.

Maybe this is simples, but I'm trying and couldn't solve... I hope someone could help me. Or, maybe, give an other ideia to the solution.

The item b), I did as following: From a), we have to find the sets $\{P_1,P_2,...,P_n\}$ such that $S_n\boxed{=}8$.

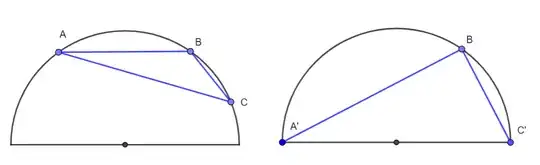
$\{(\pm1,0)\}$ is trivial and the sets of type $\{P_1,(\pm1,0)\}$ with $P_1$ on the semicircle above too, because we have a rectangle triangle and can use Pytagoras.

I've proved that I cannot have a point between $(-1,0)$ and $(1,0)$. Also, the polygon with more an angle $>90^o$ don't respect, by the argument of item a). So, we must only analyze rectangles. I did this analyse and didn't find any set.

Conclusion: $\{(\pm1,0)\}$ and the sets of type $\{P_1,(\pm1,0)\}$ with $P_1$ on the semicircle above.

What do you think? Thanks very much.

Answer 1

Let us prove that for arbitrary 3 points placed on a semicircle of unit radius, the sum $S$ of squares of their distances is less then or equal to 8.

Case 1: all three points on the diameter

It's easy to show that 3 arbitrary points shown on the left have smaller $S$ compared to the special case shown on the right ($AB<AB'$, $AC<AC'$, $BC<B'C'$

For the three points on the right:

$$S=x^2+(2-x)^2+2^2=x^2+4-4x+x^2+4=8-2x(2-x)$$

Obviously $x\le2$ so $S\le8$.

Case 2: Two points on the diameter, one point above on the circle.

Arbitrary case is shown on the left. For every such case it is possible to find a similar case, with one point on the diameter moved to the end of it, that has bigger $S$. For example, if ve move point $A$ to the left end of the diameter $BA'>BA$, $CA'>CA$. Now look at the picture on the right and triangles $A'BC$ and $A'BC'$. We want to prove that $S(A'BC)<S(A'BC'):$

$$S(A'BC)=c^2+a'^2+(2-x)^2=c^2+(a^2+x^2-2ax\cos\alpha)+4-4x+x^2=$$

$$S(A'BC)=c^2+a^2+4+2x^2-2ax\cos\alpha-4x=S(A'BC')-2x(2-x)-2ax\cos\alpha\le S(A'BC')$$

Note that $S(A'BC')=8$.

Case 3: Two points on circumference, one point on the diameter

For the triangle shown on the left, it is always possible to move one point to the end of the diameter and create a triangle that has a bigger $S$. For example, if you move point $A$ of triangle $ABC$ to point $A'$: $BA'>BA$, $CA'>CA$. So $S(ABC)\lt S(A'BC)$ and according to case (2), $S(A'BC)\le8$

Case 4: All three points on circumference

This case is trivial. Such triangle has smaller $S$ compared with triangle $A'BC'$ and according to case (2) $S(A'BC')=8$.

Answer 2

I am not great with formal proofs, but I can explain to you how I would solve both questions in an intuitive way.

a) From the definition of X, you can visualize the semi-circle (the top half of the unit-circle). We must prove that there exists a formation such that all points $P_i$ connected to each other, their euclidean distances squared (summed up) remain smaller or equal to 8.

If you don't think about the squared part, but simply, such that each points on this semi-circle is connected to the next point. How can we order these points such that the length of the total amount of line drawn between these points is minimal? Clearly, ordering the points such that connecting them criss-cross from left to right and up and down, the amount of line drawn to connect them will be a lot. However, if you place them in order such that the points follow the semi-circle, the length will be 2 (from [-1,0] to [1,0]) + pi (half of the circle).

In the case of the sum which squares the distances between each point, you have to prove that for any set of points this total must always be smaller or equal than 8. We already found previously that without squaring, following the circle, this value can be 2+pi. If we square this same solution (in which the distance between each point is <1) the squared version will be even smaller. The only way to make it larger is by only including points which are more than 1 apart, since squaring would increase this total value. Maximizing this value requires you to travel the longest distance, which squared would lead to the highest value. Travel from [-1,0] to [1,0] = 2 (squaring makes this 4). Then moving back to the original point adds another 4, equaling 8. Any other points along the semi-circle will always bring you to a value < 8.

b) Agreed with your solution. The only answers I can come up with are {[-1,0];[0,1] or any other point along the semi-circle;[1,0]} and {[-1,0];[1,0]} in which $S_n$=8 in both occasions.