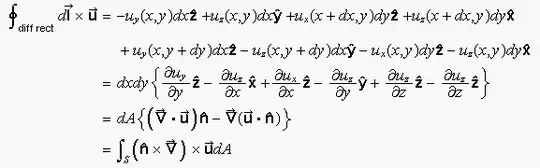2

I am working through Susan Lea's Mathematics for Physicists however I am stuck on problem 31)b):

31) Prove

b)

$\int_{S}(\hat{n}\times\vec{\nabla})\times\vec{u}\hspace{0.5mm}dA = \unicode{x222E}_{C}d\vec{l}\times\vec{u} $

I have looked at the solution and understand that first a differential rectangle is constructed in the x-y plane and the integral on the right is then broken down after applying the cross product. However I get stuck afterwards with how the cross product is computed, I use the determinant method to compute crossproducts for the first row is the x,y,z unit vectors but I believe the next two rows are done incorrectly which is why I don't get the appropriate solution:

The solution

Can someone please explain this?

QuantumPanda
  • 405
  • Can the downvoter elaborate what issue they found with my post? – QuantumPanda Aug 29 '18 at 16:25
  • More details, please? What do you know about $S$, $C$ and $u$? Is $C$ in the $x$-$y$ plane? – Robert Israel Aug 29 '18 at 16:28
  • These are all the details supplied by the problem, I have left nothing out, it is assumed for arbitrary S and C and u. The problem is simplified by assuming the x-y plane. This is a mathematical physics textbook I would like to say that this works for up to 3 dimensions x,y,and z and contour integrals are in the x-y plane. S is a surface integral. – QuantumPanda Aug 29 '18 at 16:31
  • 2
    $C$ is the boundary of $S$? $\hat{n}$ the unit normal to $S$ (in the correct orientation)? – Robert Israel Aug 29 '18 at 17:05
  • @RobertIsrael That is correct – QuantumPanda Aug 29 '18 at 19:14
  • If $\hat {\mathbf n}$ isn't a constant vector, then there might be some difficulty with the $\nabla(\mathbf u \cdot \hat {\mathbf n})$ term. A different way to write this identity is $$\int_{\partial S} \mathbf u \times d \mathbf s = \iint_S ((\nabla \cdot \mathbf u) I - (\nabla \mathbf u)^t) d \mathbf S,$$ where $\nabla \mathbf u$ is the Jacobian matrix, $(\nabla \mathbf u)_{i j} = \partial u_i / \partial x_j$, $I$ is the identity matrix, and the boundary does not have to lie in a plane. Another derivation is given here. – Maxim Aug 30 '18 at 06:32
  • This is a physics case, you should expect $\hat{n}$ to be constant – QuantumPanda Aug 30 '18 at 14:03

0 Answers0