3

A strip polyomino is a polyomino through which we can draw a path $C_1, C_2, \cdots C_k$, such that all the cells in the polyomino is in the path, and no cell is repeated in the path, and $C_i$ and $C_{i+1}$ share an edge.

(All strip polyominoes with even area are tileable by dominoes. All strip polyominoes with odd area have the same color endpoints if we apply the checkerboard coloring.)

Call a strip black if it endpoints are black. A peak is a cell with only one neighbor.

My question: Suppose $R$ and $S$ are black strip polyominoes, with all cells in $S$ also in $R$, and that $R$ has no peaks. Is $R - S$ tileable by dominoes?

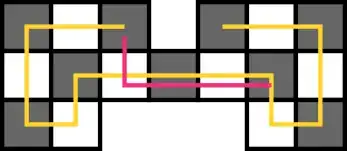
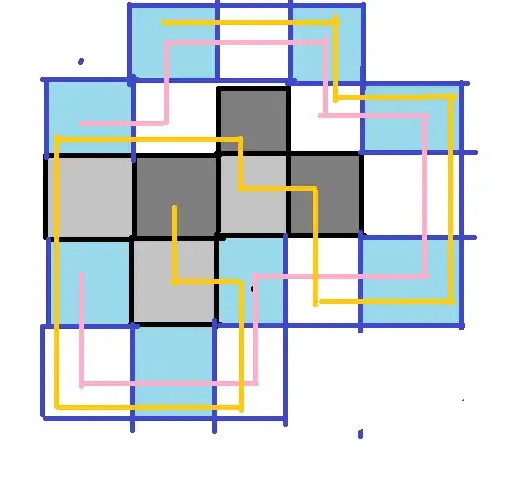
Here are two example, $R$ in yellow, and $S$ in red.

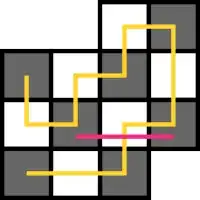
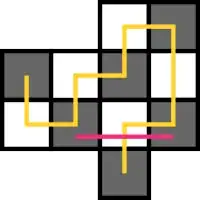
enter image description here

enter image description here

If $R$ has peaks, we can find an example where it fails:

enter image description here

Background: This idea occurred to me while trying to find a proof for this:

Is every "even" polyomino with one hole tileable by dominoes?

The idea was roughly to take $R$ has the even polyomino with the hole filled, and $S$ as the hole. Then tile $R$ by dominoes, except for the last $k$ cells along the path (where $k$ is the number of cells in $S$), and cover the last $k$ cells with monominoes. We can then shift monominoes along the path, and if everything works out just right we can position all the monominoes over the hole and so find a tiling for the remaining figure.

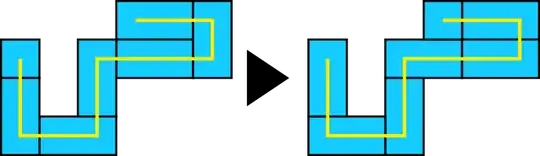
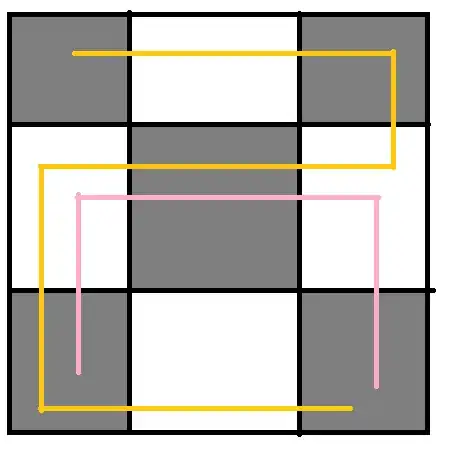
Here is what I mean with shifting a monomino:

enter image description here

(It did not work, because some even polyominoes are not strip polyominoes, for example positioning five $3\times 3$ squares in an X.)

In regions without peaks, there is always a cycle (a sequence of cells that form a path, with $C_1 = C_k$, not necessarily all the cells in the polyomino); this may be relevant. (See for example Tiling figures of the plane with two bars , proof of Theorem 3.5 p.9.)

I added the graph theory tag because it feels like slicing and splicing paths may be a way to answer the question.

Herman Tulleken
  • 3,828

1 Answers1

2

If I understand your definitions right and if you'll forgive the crude MSPaint diagram, I think this example shows that such a polyomino can be nontileable. Here the orange line traces out the strip for $R$, the pink line traces it for $S$, and the light/dark gray squares are the squares remaining in $R-S$, which are clearly non-tileable.

Polyomino

Edit: on second thought, a simpler example can be found in the 3x3 square, where $S$ is again traced out by the pink line:

3x3 square with path removed

Gregory J. Puleo
  • 6,763
  • 4
  • 25
  • 31
  • 1
    Thanks (for the second example too). After looking at these it seems very easy to find counterexamples (after I struggled with it all day). – Herman Tulleken Aug 07 '18 at 02:04
  • It was a fun problem to think about -- thanks for posting it! – Gregory J. Puleo Aug 07 '18 at 02:09
  • 2
    While it is easy to make counterexamples where $R-S$ is disconnected into odd-sized parts, having it connected but untileable is trickier. I think that makes the first counterexample rather interesting. – Jaap Scherphuis Aug 07 '18 at 09:12