1

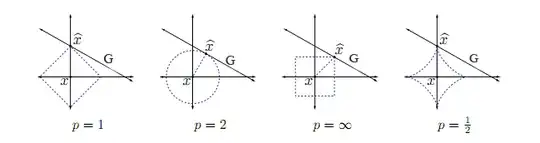
$$\begin{array}{ll} \text{minimize} & f(x) := \max \{ |x_1|,|x_2| \}\\\\ \text{subject to} & g(x) := a_1 x_1 + a_2 x_2 + b \leq 0\end{array}$$

where $f, g$ : $\mathbb{R}^{2}\rightarrow \mathbb{R}$, and $a_{1}, a_{2}, b > 0$.

Since the global minimum of $f$, $(0,0)$, does not satisfy the constraint, and since $f$ is convex, the minimum is attained on the boundary of $C:=\{x \mid g(x)\leq 0\}$. Hence, the minimizer is a point of the form

$$\left(\frac{-b-a_2x_2}{a_1},x_2\right)$$

Intuitively, I can see that at the minimum, we must have $x_1=x_2$, giving us $\left(\frac{-b}{a_1+a_2}, \frac{-b}{a_1+a_2}\right)$ as the minimizer. How can I show this rigorously?

Rodrigo de Azevedo
  • 23,223
jackson5
  • 1,674

3 Answers3

1

Let $(x_1,x_2):=(y_1,y_2)$ be a minimizing pair of $f(x_1,x_2)$ under $g(x_1,x_2)\leq 0$. Clearly, $y_1\leq 0$ or $y_2\leq0$. If $y_1<y_2$, then $$(x_1,x_2)=\left(y_1+\epsilon,y_2-\frac{a_1}{a_2}\epsilon\right)$$ is a solution for all real numbers $\epsilon$. What happens if $\epsilon$ is a very small positive real number, say $$0<\epsilon\ll\frac{y_2-y_1}{1+\frac{a_1}{a_2}}\,?$$ Do something similar when $y_1>y_2$.

Batominovski
  • 50,341
1

Generalizing and rephrasing slightly, we have the following optimization problem in $\mathrm x \in \mathbb R^n$

$$\begin{array}{ll} \text{minimize} & \| \mathrm x \|_{\infty}\\ \text{subject to} & \mathrm a^\top \mathrm x \leq b\end{array}$$

where vector $\mathrm a \in \mathbb R^n$ has no zero entries. There are two cases to consider:

  • If the origin is in the feasible region, then the minimum is attained at the origin.

  • If the origin is not in the feasible region, then the minimum is attained at its boundary.

Hence, in the latter case, we have a least-norm problem in the $\infty$-norm

$$\begin{array}{ll} \text{minimize} & \| \mathrm x \|_{\infty}\\ \text{subject to} & \mathrm a^\top \mathrm x = b\end{array}$$

In $\mathbb R^2$, the feasible region of this least-norm problem is a line that is neither vertical nor horizontal (due to the restrictions on vector $\mathrm a \in \mathbb R^2$). We would like to find the point on this line that is closest to the origin in the $\infty$-norm. Since the level sets of $\| \mathrm x \|_{\infty}$ are squares centered at the origin, then the minimizer is a square's vertex and, thus, its entries have the same absolute value.

enter image description here

[ image source ]

Rodrigo de Azevedo
  • 23,223
1

As we can observe in the attached figures for

$$ \min\left(\max\left(|x|,|y|\right)\right)\;\;\mbox{s. t.}\;\; ax+by + c\le 0 $$

with $a = -2,b = 1, c = 6$ first a spatial representation and second as the level surfaces and the feasible region in light blue,

enter image description here enter image description here

if the origin is at the feasible region interior the the answer is $0$ otherwise the answer is at one of the solutions

$$ ax+by+c=0\\ x+y = 0 $$

and

$$ ax+by+c=0\\ x-y = 0 $$

or at

$$ \min\left(\left|\frac{c}{a-b}\right|,\left|\frac{c}{a+b}\right|\right) $$

Cesareo
  • 36,341