Expected number of cycles in random function

Question

Let f be a left-total function with a discrete domain and codomain both in the range of 0..N. The image of f is chosen randomly (with replacement). Given N, how many cycles is the function expected to contain?

Edit: Here's the code

from random import randint


def test(N):
    """Returns all cycles for a function over 0..N-1"""
    edges = [randint(0,N-1) for n in range(N)]

    cycles = []

    def cycle(start):
        """Find a cycle from a given start point"""
        current = start
        lst = []
        while True:
            if current in lst:
                lst = lst[lst.index(current):]
                break
            lst.append(current)
            current = edges[current]
        return lst

    # For every edge from domain to codomain:
    # append the cycle to the list if it isn't contained already
    for e in edges:
        c = cycle(e)
        #if c is not None:
        srt = sorted(c)
        if not srt in cycles:
            cycles.append(srt)

    #Print function
    #for i,e in enumerate(edges):
    #    print(f"{i} -> {e}")

    # Print N and the number of cycles in this function
    #print(N, cycles)

    return len(cycles)

# Get the average number of cycles for N=1..200
for n in range(1,200):
    avg = []
    # 1000 random functions of size N
    for i in range(1000):
        avg.append(test(n))
    #print(avg)
    print("%i\t%f" % (n, sum(avg)/len(avg)))

With values:

1   1.000000
10  1.966000
20  2.191000
30  2.356000
40  2.573000
50  2.635000
60  2.742000
70  2.762000
80  2.932000
90  2.851000
100 3.002000

Answer 1

Let $a_n$ denote the expected number of cycles in a random endofunction on a set of $n$ elements. Marko Riedel has already posted the derivation of the asymptotic result $a_n\sim\frac12\log n$ by P. Flajolet and A. Odlyzko in a comment. Here I'll also derive the constant term, and I'll use Prüfer sequences instead of generating functions, so you can choose the proof that's more accessible for you.

Joyal's proof of Cayley's formula for the number of labeled trees with a given number of vertices makes use of a correspondence between endofunctions and vertebrates. A vertebrate is a tree with an ordered pair of (possibly identical) vertices distinguished. The name is based on the idea that the unique path in the tree connecting the two distinguished vertices forms a sort of spine of the tree.

An endofunction can be viewed as a family of rooted trees, where the roots are the elements contained in cycles. A vertebrate can also be viewed as a family of rooted trees, where the roots are the elements along the spine. There are $k!$ possible orders of the $k$ elements along the spine, and $k!$ possible permutations specifying the endofunction on the $k$ elements contained in cycles, so there are as many endofunctions with $k$ cyclic elements as there are vertebrates with spine length $k$.

To count the vertebrates with spine length $k$, label the vertices $1$ through $n$ and fix the spine to be $n,n-1,\ldots,n-k+2,m$, in that order, with $m\lt n-k+2$ arbitrary. Then the last $k-2$ elements of the Prüfer code for the vertebrate are $n-k+2,\ldots,n-1$, and the element before that is one of the $k$ elements on the spine; the remaining $n-k-1$ elements of the Prüfer code can be chosen arbitrarily. We also need to multiply by $\frac{n!}{(n-k)!}$ because we arbitrarily fixed the $k$ elements on the spine, so the number of vertebrates with spine length $k$ (and thus the number of endofunctions with $k$ cyclic elements) is

$$ kn^{n-k-1}\frac{n!}{(n-k)!}=(n-1)!\frac{kn^{n-k}}{(n-k)!}\;. $$

The endofunction permutes the $k$ cyclic elements with some permutation on $k$ elements. The expected number of cycles in a uniformly random permutation on $k$ elements is $H_k=\sum_{j=1}^k\frac1j$, the $k$-th harmonic number. (This is proved e.g. here.)

Thus, the expected number of cycles in a uniformly random endofunction is

$$ a_n=\frac{\sum_{k=1}^n(n-1)!\frac{kn^{n-k}}{(n-k)!}\sum_{j=1}^k\frac1j}{\sum_{k=1}^n(n-1)!\frac{kn^{n-k}}{(n-k)!}}\;. $$

The denominator is of course simply the total number $n^n$ of endofunctions. Exchanging the summations yields:

\begin{eqnarray*} a_n&=&n^{-n}\sum_{k=1}^n(n-1)!\frac{kn^{n-k}}{(n-k)!}\sum_{j=1}^k\frac1j \\&=& (n-1)!\sum_{j=1}^n\frac1j\sum_{k=j}^n\frac{kn^{-k}}{(n-k)!} \\ &=& n!\sum_{j=1}^n\frac1j\frac{n^{-j}}{(n-j)!}\;. \end{eqnarray*}

The last equality is provided by Wolfram|Alpha; I haven't tried to prove it, but if you're interested I suspect there's a nice combinatorial argument for it.

I doubt this can be simplified further, but we can derive an upper bound and an asymptotic result from it.

For the upper bound, note that $\frac{n!n^{-j}}{(n-j)!}\le1$, so $a_n\le\sum_{j=1}^n\frac1j=H_n=\log n+\gamma+o(1)$, where $\gamma$ is the Euler–Mascheroni constant.

For the asymptotics, I won't rigorously derive the order of the approximations, but the result should be correct up to terms of order $o(1)$.

We have

\begin{eqnarray*} a_n &=& n!\sum_{j=1}^n\frac1j\frac{n^{-j}}{(n-j)!} \\ &=& \sum_{j=1}^n\frac1j\prod_{k=0}^{j-1}\frac{n-k}n \\ &=& \sum_{j=1}^n\frac1j\prod_{k=0}^{j-1}\left(1-\frac kn\right) \\ &=& \sum_{j=1}^n\frac1j\exp\left(\sum_{k=0}^{j-1}\log\left(1-\frac kn\right)\right) \\ &\approx& \sum_{j=1}^n\frac1j\exp\left(-\sum_{k=0}^{j-1}\frac kn\right) \\ &=& \sum_{j=1}^n\frac1j\exp\left(-\frac{j(j-1)}{2n}\right) \\ &\approx& \sum_{j=1}^\infty\frac1j\exp\left(-\frac{j(j-1)}{2n}\right)\;. \end{eqnarray*}

Thus we want to sum the harmonic series, damped by a Gaussian. This is hard to do directly because of the smooth transition from the discrete behaviour for small $j$ that we need to sum exactly to the approximately continuous behaviour for large $j$ that we could approximate with an integral. To deal with these two domains separately, we can introduce an intermediate term with a simple exponential that we can sum exactly:

\begin{eqnarray*} a_n&\approx&\sum_{j=1}^\infty\frac1j\exp\left(-\frac{j(j-1)}{2n}\right) \\ &=& \sum_{j=1}^\infty\frac1j\exp\left(-\frac j{\sqrt{2n}}\right)+\sum_{j=1}^\infty\frac1j\left(\exp\left(-\frac{j(j-1)}{2n}\right)-\exp\left(-\frac j{\sqrt{2n}}\right)\right)\;. \end{eqnarray*}

The first sum is the integral of a geometric series:

$$ \sum_{j=1}^\infty\frac{q^j}j=\int_0^1\sum_{j=1}^\infty q^{j-1}\mathrm dq=\int_0^1\frac1{1-q}\,\mathrm dq=-\log(1-q)\;, $$

and

$$ -\log\left(1-\exp\left(-\frac1{\sqrt{2n}}\right)\right)\approx\log\sqrt{2n}=\frac12(\log n+\log2)\;. $$

The summand in the second sum has no singularity at $j=0$ and varies smoothly, so we can approximate it by an integral over $x=\frac j{\sqrt{2n}}$:

\begin{eqnarray*} a_n&\approx&\frac12(\log n+\log2)+\int_0^\infty\frac1x\left(\mathrm e^{-x^2}-\mathrm e^{-x}\right)\mathrm dx \\ &=&\frac12(\log n+\log2+\gamma)\;, \end{eqnarray*}

where the last equality is again provided by Wolfram|Alpha.

A plot of the exact values against $\log n$, compared to the linear asymptote, confirms the asymptotic result:

P.S.:

We can use the same method to obtain an asymptotic result for the expected length of the cycle that a uniformly random element in a uniformly random endofunction leads to. The element is equally likely to lead to any one of the cyclic elements, so the expected length of the cycle is the expected length $\frac{k+1}2$ of the cycle containing a random cyclic element:

$$ n^{-n}\sum_{k=1}^n(n-1)!\frac{kn^{n-k}}{(n-k)!}\cdot\frac{k+1}2=\frac12+\frac{n!}{2n}\sum_{k=1}^n\frac{k^2n^{-k}}{(n-k)!}\;. $$

Here we don't have any complication due to a singularity at the origin, and we can directly approximate the sum by an integral over $x=\frac k{\sqrt{2n}}$ as above, yielding

$$ \frac{n!}{2n}\sum_{k=1}^n\frac{k^2n^{-k}}{(n-k)!}\approx\frac1{2n}(2n)^{\frac32}\int_0^\infty x^2\mathrm e^{-x^2}\mathrm dx=\sqrt{\frac{\pi n}8}\;. $$

I didn't include the constant term $\frac12$ because the approximations also contribute a constant term; the correct constant term seems to be $\frac13$. Here's a log-log plot of the exact values compared to the asymptote $\sqrt{\frac{\pi n}8}$ and to $\sqrt{\frac{\pi n}8}+\frac13$:

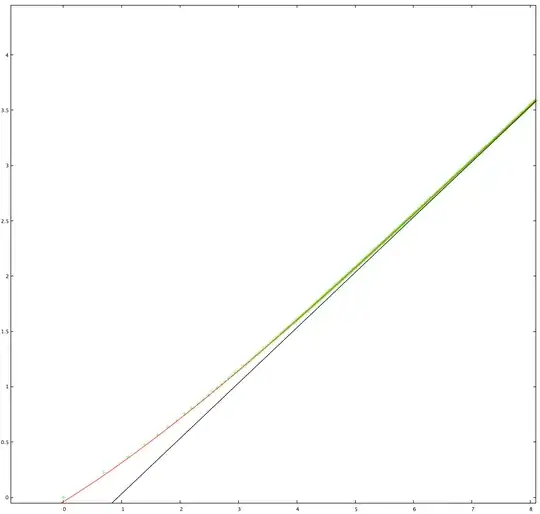
So the expected number of cycles is of order $\log\sqrt n$, compared to $\log n$ for permutations, and the expected length of the cycle containing a random element is of order $\sqrt n$, compared to $n$ for permutations.

The number $k$ of cyclic elements is directly related to the expected length $\frac{k+1}2$ of the cycle containing a random element, so its expected value is asymptotically $\sqrt{\frac{\pi n}2}$, as also derived in the paper by Flajolet and Odlyzko.