The Abel-and-Cain Urn Problem

Question

An urn contains three distinguishable kinds of balls, say $A,B,C$.

Abel bets to get, in $t$ trials with replacement, at least one ball of kind $A$ and at least one ball of kind $B$.

Cain bets to get, in $t$ trials with replacement, exactly $t$ balls of kind $C$.

We want Abel and Cain to have the same chance to win.

My solution is: No matter the number of balls of each kind in the urn, if Abel and Cain have the same chance to win at the end of the game, then it must be $t=2$.

My reasoning is: Abel can win at any trial between $2$ and $t$, whereas Cain can possibly win only at the end of the game. Since we asked that at the end of the game Abel and Cain must have the same chance to win, then the last trial must represent the only possible success also for Abel, and this implies $t=2$.

Is this reasoning correct?

A further question, which might be a bit naive (or even silly), so please apologize me in that case:

How do we take into account (e.g. in terms of conditional probability) the fact that Cain already knows that Abel cannot win at the first trial and that Abel already knows that Cain cannot win at any trial a part the last one?

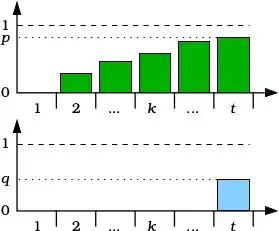
EDIT: I attach this scheme to explain the reasoning (see also the comments for further details).

Here we interpret each trial as a shot. And the probability to get a success for Abel in each trial $k$ as a target of a certain area (green targets, top scheme). The area of the $Ab_k$ targets increases as $k$ increases, and the area of the target in correspondence of $t$ is $Ab_t=p$. For Cain, there is only one target (blue target, bottom scheme), the last one, since he cannot win in the middle of the game. The area of his last target is $Ca_t=q$.

The request is that $p=q$, in correspondence of the last trial. Now, Abel can hit a target (and therefore win the game) at any trial (a part the first one). So if the last one has the same area for Abel and Cain, there must be only one target, otherwise Abel has more chance to win.

I think your conclusion that $t=2$ is correct but I don't think your reasoning supports that conclusion. I believe there is a link between this problem and Fermat's Last Theorem. — gandalf61, Jun 27 '18 at 09:16
Thanks @gandalf61! I also think that the reasoning is not correct (that's why I posted the question!). But, what is wrong there? — , Jun 27 '18 at 09:47
Let $p_i$ denote the probability that Abel arrives for the first time at a winning position at trial $i$. Likewise let $q_i$ denote the probability that Cain arrives for the first time at a winning position at trial $i$. Then $p:=p_1+p_2+\cdots+p_t$ is the probability that Abel wins and $q:=q_1+q_2+\cdots+q_t$ is the probability that Cain wins. So Abel and Cain have equal chance to win if $p=q$. Further we have $p_1=0$ and $q_1=\cdots=q_{t-1}=0$. So $p=p_2+\cdots+p_t$ and $q=q_t$ and the condition $p=q$ is the same as $p_2+\cdots+p_t=q_t$. — drhab, Jun 27 '18 at 10:49
@drhab But you wrote yourself in your answer that $(b+c)^t+(a+c)^t=(a+b+c)^t$. Doesn't this mean $p_t=q_t$? — , Jun 27 '18 at 10:55
No. It means $P(Ab)=P(Cain)$ or in terms of my former comment: $p=q$. — drhab, Jun 27 '18 at 10:58
So. The probability that Abel wins $1-\left(\frac{a+c}{a+b+c}\right)^t-\left(\frac{b+c}{a+b+c}\right)^t+\left(\frac{c}{a+b+c}\right)^t$ (from Bayes' theorem). The probability that he wins at the trial $k$ is $1-\left(\frac{a+c}{a+b+c}\right)^k-\left(\frac{b+c}{a+b+c}\right)^k+\left(\frac{c}{a+b+c}\right)^k$. The probability that Cain wins is $\left(\frac{c}{a+b+c}\right)^t$. Therefore it really seems to me that the request is $p_t=q_t$. — , Jun 27 '18 at 11:05
I see. You used the sum of the geometric progression. However, let $P(A_t)$ the pr. to get at least one element of kind $A$ in $t$ trials, and $P(B_t)$ the pr. to get at least one element of kind $B$ in $t$ trials. $p_t=P(A_t\cap B_t)=P(A_t|B_t)P(B_t)=[1-P(\overline{A_t}|B_t)]P(B_t)=P(B_t)-P(\overline{A_t}|B_t)P(B_t)=P(B_t)-P(B_t|\overline{A_t})P(\overline{A_t})=1-\left(\frac{a+c}{a+b+c}\right)^t-\left[1-\left(\frac{c}{b+c}\right)^t\right]\left(\frac{b+c}{a+b+c}\right)^t=1-\left(\frac{a+c}{a+b+c}\right)^t-\left(\frac{b+c}{a+b+c}\right)^t+\left(\frac{c}{a+b+c}\right)^t$. — , Jun 27 '18 at 11:29
What you wrote (not in last comment, but before) as probability that Abel wins at trial $k$ is in fact the probability that Abel wins in one of the trials $1,2,\dots,k$. Try it out for $k=3$ to confirm yourself. — drhab, Jun 27 '18 at 11:29
Ok. But what about the reasoning with Bayes' theorem? Before I just wrote $p_k=P(A_k\cap B_k)$. — , Jun 27 '18 at 11:31
@drhab Did I clarified a bit with the picture I added? I miss the old, good blackboard... It's not easy to discuss like this. This makes me appreciating your efforts even more. Thanks! — , Jun 27 '18 at 11:45
Your calculation using Bayes is correct and agrees with my answer. It calculates the probability that after $t$ trials at least one element of type $A$ and at least one element of type $B$ is selected. Not the probability though that this happens after $t$ trials and has not happened yet after $t-1$ trials. So I would classify it as $p$ and not as $p_t$. — drhab, Jun 27 '18 at 11:50
@drhab Sorry, I am not the sharpest knife in the drawer, but I don't get it. $P(A_t\cap B_t)$ is the probability that, at the trial $t$, Abel wins the game, no matter what happened before. It seems to me that there is no actual difference between $p=q$ and $p_t=q_t.$ — , Jun 27 '18 at 11:55
@drhab Actually, is not difficult to show that $P(\bigcup_{k=2}^t A_k\cap B_k)=P(A_t\cap B_t)$ — , Jun 27 '18 at 12:08
Let it be that $t=3$ and $a=b=c=1$. Then $p_2=P(AB)+P(BA)=2\frac13\frac13=\frac29$ and $p_3=P(CAB)+P(CBA)+P(ACB)+P(BCA)+P(AAB)+P(BBA)=6\frac13\frac13\frac13=\frac29$ so that $p_2+p_3=\frac49=1-(\frac23)^3-(\frac23)^3+(\frac13)^3=p\neq p_3$. We have $p=p_2+p_3$ and $q=q_3$ so $p=q$ is not the same statement as $p_3=q_3$. — drhab, Jun 27 '18 at 12:08
Again $p_i$ is the probability of the event that Abel is at trial $i$ in a winning position for the first time (so it does matter what happened before). — drhab, Jun 27 '18 at 12:15
@drhab Ok. I have to think about it. I reckon that your $p_i$ are not the same as the areas of the picture above. That is likely the reason of the misunderstanding. My $p_k$ are the areas, i.e. the probabilities to win at the trial $k$, not the probabilities to win for the first time at the trial $k$. — , Jun 27 '18 at 12:18
@drhab But then your $p_i$ should be something like $P(A_i \cap B_i|\overline{A_{i-1}\cap B_{i-1}})$, right? — , Jun 27 '18 at 12:25
@drhab I evaluated "your" $p_k=P(A_k\cap B_k|\overline{A_{k-1}\cap B_{k-1}})$. From Bayes, $P(A_k\cap B_k|\overline{A_{k-1}\cap B_{k-1}})P(\overline{A_{k-1}\cap B_{k-1}})=P(\overline{A_{k-1}\cap B_{k-1}}|A_k\cap B_k)P(A_k\cap B_k)=[1-P(A_{k-1}\cap B_{k-1}|A_k\cap B_k)]P(A_k\cap B_k)=P(A_k\cap B_k)-P(A_{k-1}\cap B_{k-1}|A_k\cap B_k)P(A_k\cap B_k)=P(A_k\cap B_k)-P(A_k\cap B_k|A_{k-1}\cap B_{k-1})P(A_{k-1}\cap B_{k-1})=P(A_k\cap B_k)-P(A_{k-1}\cap B_{k-1})$. Therefore, $p_k=\frac{P(A_k\cap B_k)-P(A_{k-1}\cap B_{k-1})}{1-P(A_{k-1}\cap B_{k-1})}$. — , Jun 27 '18 at 15:02
And also $p_t=\frac{P(A_t\cap B_t)-P(A_{t-1}\cap B_{t-1})}{1-P(A_{t-1}\cap B_{t-1})}$. Do you confirm? — , Jun 27 '18 at 15:03
If we wish $P(A_t\cap B_t)=P(Ca)$, we must write $\frac{P(A_t\cap B_t)-P(A_{t-1}\cap B_{t-1})}{1-P(A_{t-1}\cap B_{t-1})}=P(Ca)$, i.e. $P(A_{t-1}\cap B_{t-1})=\frac{P(A_t\cap B_t)-P(Ca)}{1-P(Ca)}$. Therefore, substituting, $$ P(A_{t-1}\cap B_{t-1})=\frac{1-\left(\frac{a+c}{a+b+c}\right)^t-\left(\frac{b+c}{a+b+c}\right)^t+\left(\frac{c}{a+b+c}\right)^t-\left(\frac{c}{a+b+c}\right)^t}{1-\left(\frac{c}{a+b+c}\right)^t} $$ $$ P(A_{t-1}\cap B_{t-1})=\frac{1-\left(\frac{a+c}{a+b+c}\right)^t-\left(\frac{b+c}{a+b+c}\right)^t}{1-\left(\frac{c}{a+b+c}\right)^t}. $$ — , Jun 27 '18 at 16:28
@drhab Therefore, in the hypothesis $1-\left(\frac{a+c}{a+b+c}\right)^t-\left(\frac{b+c}{a+b+c}\right)^t=0$, we have $P(A_{t-1}\cap B_{t-1})=0$. Which is true if and only if $t=2$. — , Jun 27 '18 at 16:29
Naturally, I meant "If we wish $p_t=P(Ca)$"... But I guess this should be discussed! : ) — , Jun 27 '18 at 16:51
@drhab In fact, I think that you meant that Abel and Cain have the same chance to win if $\sum_{k=2}^t p_k=P(Ca)$, using "your" $p_k$, isn't it? — , Jun 27 '18 at 17:05
Sorry, but I am afraid that I sent you into the wrong direction by confirming that my $p_i$ should be something like $P(A_i\cap B_i\mid \overline{A_{i-1}\cap B_{i-1}})$. That is not true. My $p_i$ equals $P((A_i\cap B_i)\cap(A_{i-1}\cap B_{i-1})^{\complement})$ — drhab, Jun 27 '18 at 17:24
@drhab I see. No problem. Thanks for the nice discussion here! — , Jun 27 '18 at 17:26
@drhab It is the final condition with your $p_k$ that must be clear to me. Abel and cain have the same chance to win if $\sum_{k=2}^t p_k=P(Ca)=\left(\frac{c}{a+b+c}\right)^t$, right? — , Jun 27 '18 at 17:28
Yes, that is what I tried to make clear in my answer. This without any mentioning "my" $p_i$. What is noted as $P(Ab)$ is in fact $\sum_{k=2}^tp_k$ where $p_k$ is the probability that Abel comes in a winning position for the first time as trial $k$. — drhab, Jun 27 '18 at 17:48
@drhab $p_k=P(A_k\cap B_k\cap\overline{A_{k-1}\cap B_{k-1}})=P(\overline{A_{k-1}\cap B_{k-1}}|A_k\cap B_k)P(A_k\cap B_k)=P(A_k\cap B_k)-P(A_{k-1}\cap B_{k-1}|A_k\cap B_k)P(A_k\cap B_k)=P(A_k\cap B_k)-P(A_k\cap B_k|A_{k-1}\cap B_{k-1})P(A_{k-1}\cap B_{k-1})=P(A_k\cap B_k)-P(A_{k-1}\cap B_{k-1})$. Therefore $\sum_{k=1}^t p_k=\sum_{k=2} ^tp_k=\sum_{k=2}^t P(A_k\cap B_k) - \sum_{k=2}^t P(A_{k-1}\cap B_{k-1})=P(A_t\cap B_t)=P(Ab)$. Right? — , Jun 27 '18 at 19:01
Yes. But for finding $p_k=P(A_k\cap B_k)-P(A_{k-1}\cap B_{k-1})$ there is shorter route: $A_{k-1}\cap B_{k-1}\subseteq A_k\cap B_k$ and if $U\subseteq V$ then $V=U\cup(V\cap U^{\complement})$ where $U$ and $V\cap U^{\complement}$ are disjoint. Then $P(V)=P(U)+P(V\cap U^{\complement})$ or equivalently $P(V\cap U^{\complement})=P(V)-P(U)$. Let us stop here Andrea. The length of our discussion is already a bit out of proportion. Cheers :-). — drhab, Jun 28 '18 at 07:02

drhab · Answer 1 · 2018-06-28T09:43:20.217

3

I do not understand your reasoning, and think that is not correct.

If I am wrong in this then it seems that you found a nice way to prove Fermat's last theorem.

That would be wonderful of course, but I have not much hope.

Let $a,b,c$ denote number of balls of kind $A$, $B$, $C$ respectively.

Let $A$ denote the event that after $t$ trials at least one of the selected balls will be of kind $A$.

Let $B$ denote the event that after $t$ trials at least one of the selected balls will be of kind $B$.

Let $Ab$ denote the event that Abel wins.

Let $Ca$ denote the event that Cain wins.

Then: $$P(Ab)=1-P(A^{\complement}\cup B^{\complement})=1-P(A^{\complement})-P(B^{\complement})+P(A^{\complement}\cap B^{\complement})=$$$$1-\left(\frac{b+c}{a+b+c}\right)^t-\left(\frac{a+c}{a+b+c}\right)^t+P(Ca)$$

So

$$P(Ab)=P(Ca)\iff(b+c)^t+(a+c)^t=(a+b+c)^t$$

edited Jun 28 '18 at 09:43

answered Jun 27 '18 at 09:13

drhab

153,781

Thanks @drhab! That's nice. But (as, I asked to @gandalf61), can you help me to point out where is the mistake in the reasoning? Which part of it you don't understand it? – Jun 27 '18 at 09:50
I don't see why the last trial represents the only possible succes for Abel. Why not e.g. $3$ trials with scores like $ABB$ (Abel wins which is clear after two trials) $BBA$ (Abel wins which is clear at last trial) and $CCC$ (Cain wins). Btw (aside), if the number of balls of sort $C$ is $0$ then both have equal chance to win if $t=1$. – drhab Jun 27 '18 at 09:57
Sure! Well, imagine each trial as a shot. And the probability to get a success for $Ab$ in each trial $k$ as a target of a certain area. The height of the $Ab_k$ targets increases as $k$ increases. The height of the target in correspondence of $t$ is $Ab_t=p$. For Cain, there is only one target (he cannot win in the middle of the game): the final one. The height of his last target is also $Ca_t=Ab_t=p$. But Abel can hit one target (and therefore win the game) at any other trial (a part the first one). So if the last one has the same height for Abel and Cain, there must be only one target. – Jun 27 '18 at 10:03
otherwise Abel has more chance to win. – Jun 27 '18 at 10:09
Sorry, substitute the word "height" with the word "area" in the previous comments! – Jun 27 '18 at 10:13
1

Let's look at it for $t=4$. For Abel there is a tuple $(0,p_2,p_3,p_4)$ where $p_i$ denotes the probability of winning at trial $i$. For Cain there is a tuple $(0,0,0,q_4)$ where $q_i$ denotes the probability at winning at trial $i$. Then the probability for Abel to win is $p_2+p_3+p_4$ and for Cain it is $q_4$. Why should $p_2+p_3+p_4=q_4$ be impossible?? – drhab Jun 27 '18 at 10:17
I don't think we can sum the probabilities. However, the point is that $p_4=q_4$. Check the picture I added in the OP: The request is that $p=q$! – Jun 27 '18 at 10:25
We can sum up the probabilities. This because we are dealing with events that are mutually exclusive. Again for $t=4$: here $p_2=P(AB\cup BA)$ and $p_3=P(AAB\cup ACB\cup BBA\cup BCA)$. If Abel wins at second trial then he wins not at third or fourth. Further $p=p_2+p_3+p_4$ and $q=q_4$, and requested is $p=q$. – drhab Jun 27 '18 at 10:33
But the request is $p_4=q_4$! – Jun 27 '18 at 10:36
1

The request is that "Abel and Cain have same chance to win": $p=q$. Not that at the last trial they have the same chance to win ($p_4=q_4$) (which can only happen if Abel has not won yet in former trials). This is my last comment on this. – drhab Jun 27 '18 at 10:39
That's a pity. But thank you very much for your contributions! – Jun 27 '18 at 10:43
I mean comment on this answer. I have placed a comment at your question. You are welcome. – drhab Jun 27 '18 at 10:51

score 2 · Accepted Answer · answered Jun 28 '18 at 01:26

2

If you replace the urn with a magical process that returns a ball $A$ or a ball $B$ with probability $a=b=1 - 2^{-1/3}$ each and a ball $C$ with probability $c=-1 + 2^{2/3}$ then you can copy paste your reasoning without any change. At no point does your reasoning make use of the fact that $a,b,c$ were supposed to be rationals.

However, with $t=3$ the probability that Abel wins is $1-(b+c)^3-(a+c)^3+c^3 = 1 - 1/2 - 1/2+c^3 = c^3$, which is also the probability that Cain wins.

Since your reasoning proves something false, it is invalid.

answered Jun 28 '18 at 01:26

mercio

51,119

Thanks for your answer! Consider $P(Cain)=\left(\frac{c}{a+b+c}\right)^t$. The numerator represents the number $c^t$ of ways in which we can extract $c$ indexed elements in $t$ ordered trials, in case the order of the trials matters. The trials involve the extraction of 1 distinguishable element at a time, i.e. imply a bijection between the trials and the elements of the urn. Your magical process does not allow, for instance, to extract exactly $t$ elements in $t$ trials, because real numbers are not indexable. What do you think? – Jun 28 '18 at 01:56
Similarly, the events $A_t$, $B_t$, require the possibility that each element could be chosen singularly ("at least one"). Therefore, sure you can invent probabilities that are real numbers, but I think that they do not represent the events in study, and are therefore unrelated to the Abel-Cain problem. – Jun 28 '18 at 02:13
@andrea.prunotto - mercio's system certainly makes it possible to extract exactly $t$ elements in $t$ trials since you allow elements to be repeated. Indeed there may be only three elements but the third (C) is about $2.847\ldots$ times as likely to be extracted as each of the other two – Henry Jun 28 '18 at 09:59
@Henry Thanks for your observation. My concern is only the fact that if we cannot establish a one-to-one correspondence between the trials and the elements, then we are not describing the events involved in this problem but something else, which is perfectly feasible and correct (only, is not the Abel-Cain Urn Problem). What's your view? – Jun 28 '18 at 10:48
@andrea.prunotto - My view is that mercio's example shows that it is possible for Abel to win early in a case where the overall probabilities of Abel winning and Cain winning are equal; this means that you cannot just assert that this is impossible. mercio's example's probabilities are irrational (hence your comments) so your claimed proof would need to use rationality explicitly; drhab's answer does this, via Fermat's Last Theorem – Henry Jun 28 '18 at 13:41
@Henry Sorry, I did not understand well your comment (consider that I am not an expert in this field). Please, can you rephrase it? Thanks for your patience!!! – Jun 28 '18 at 14:01

The Abel-and-Cain Urn Problem

2 Answers2

Linked