Let us approximate a discrete distribution by a standard normal distribution, without using a continuity correction factor. Let $X$ be a random variable with discrete distribution, and $Y$ be a random variable with standard normal distribution. Since we did not use a continuity correction factor, can we say that the $P(X \geq x)$ is always greater than or equal to its approximated probability by the standard normal distribution?
-
Yes, for normal approximations to binomial. Details and an example in my Answer below. – BruceET Jun 18 '18 at 09:29
-
No (did you intend less than or equal?) - take the simple example of tossing two fair coins and letting $X$ be the number of heads. Then $P(X \gt 1) = \frac14$ for two heads, while the normal approximation at the expectation of $1$ would suggest $\frac12$ – Henry Jun 18 '18 at 14:28
2 Answers
If the discrete random variable $X$ takes integer values, then $$P(X > x)= P(X \ge x+1) = P(X \ge x+.5)$$ The continuity correction would use the third expression when using a continuous distribution as an approximation.
Ordinarily, the approximating continuous distribution would have positive probability in the interval $[x, x+.5].$ In that case using the continuity correction will give you a smaller approximated value.
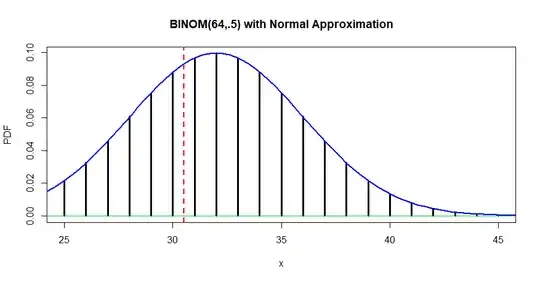
Example: Suppose $X \sim \mathsf{Binom}(n = 64, p = 1/2)$ and you seek $P(X > 30).$ The exact value is $P(X > 30) = 1 - P(X \le 30) = 0.6460096.$
1 - pbinom(30, 64, .5)
## 0.6460096
If you use $P(X^\prime > 30) = 1 - P(X^\prime \le 30)$ as an approximation, where $X^\prime \sim \mathsf{Norm}(\mu = 32, \sigma=4),$ you will get $P(X > 300) \approx 0.6914625.$
1 - pnorm(30, 32, 4)
## 0.6914625
But if you use the continuity correction, you will use $P(X^\prime > 30.5) = 1 - P(X^\prime \le 30.5) = 0.6461698.$ Hence, your approximation will be $P(X > 30) \approx 0.6461698.$ This is smaller than the value 0.6914625 without the continuity correction. It is also closer to the exact binomial probability.
1 - pnorm(30.5, 32, 4)
## 0.6461698
Usually in textbook examples you can expect about two decimal places of accuracy from a continuity-corrected normal approximation to a binomial distribution. To four decimal places, the exact value in this example is 0.6460 and the continuity-corrected normal approximation is 0.6462. (Here we get three-place accuracy; approximations are often best when $p \approx 1/2.$)
The figure below shows relevant binomial probabilities (vertical bars) and the approximating normal density curve. Notice that be binomial probability $P(X = 31)$ is approximated by the area under the normal curve above the interval $[30.5, 31.5].$ The uncorrected approximation wrongly includes the vertical strip between $x = 30.0$ and $x=30.5$ under the normal curve.
Note: The values I have shown are from R statistical software. If your normal approximations are obtained by standardization and using a printed normal table, then results will be slightly different because of the rounding entailed in the use of the table.
- 52,418
-
Thank you. So you mean that we can't say for sure that P(X>=n) is greater than its approximated value by normal distribution? – Carol Jun 18 '18 at 17:31
-
I checked P(X>=n) and normal distribution always gives the smaller value. Is there any intuition or proof behind that? – Carol Jun 18 '18 at 17:50
-
I'm agreeing with you. The difference in my example is the area under the normal curve above the interval $[30.0, 30.5],$ as mentioned just before the figure. To four places, compare normal probabilities $P(X^\prime > 30) = 0.6915$ without continuity correction with $P(X^\prime > 30.5) = 0.6462$ with continuity correction. For intuition, start with obvious fact that $P(X^\prime > 30) > P(X^\prime > 30.5).$ (Maybe shade in the two areas under the normal curve.) – BruceET Jun 18 '18 at 21:47
-
Thank you. I mean the probability value when we don't use continuity correction factor is always less than the "true probability value" for P(X >= x). In fact, without using correction factor we are underestimating the true probabilities. – Carol Jun 19 '18 at 01:42
-
Now you've changed it to $P(X \ge x),$ which is a slightly different situation. I have tried to set the principles out clearly in my answer, and I'll leave the variations to you. – BruceET Jun 19 '18 at 02:17
Hint:
Consider a binomial distribution with parameters $n, p$.
- What is $P(X \gt n)$ for the actual binomial distribution?
- Is the normal approximation less than or equal to this?
- 169,616