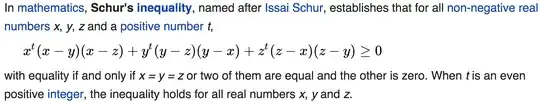-1

enter image description here

It's easy to show that if $x=y=z$ or two of them are equal and the other is zero, then the equality holds. What about the other direction?

EDIT: I think this is more like a combinatorial problem. To prove if the equality holds, then $x=y=z$ or two of them are equal and the other is zero. That is $$x^t(x-y)(x-z) + y^t(y-z)(y-x)+z^t(z-x)(z-y)=0 \implies (x=y=z) \text{ or } (x=y \text{ and } z=0)\\ \equiv \cdots \implies (x=y \text{ and } y=z \text{ and } x=z) \text{ or } (x=y \text{ and } z=0).$$

To prove the contrapositive, we need to prove $$\neg(x=y \text{ and } y=z \text{ and } x=z) \text{ and } \neg(x=y \text{ and } z=0) \implies x^t(x-y)(x-z) + y^t(y-z)(y-x)+z^t(z-x)(z-y)=0\\ \equiv (x\not =y \text{ or } y\not =z \text{ or } x\not =z) \text{ and } (x\not =y \text{ or } z\not =0) \implies x^t(x-y)(x-z) + y^t(y-z)(y-x)+z^t(z-x)(z-y) \not=0.$$ There are $(3+3+1)(2+1)=21$ possibilities of the hypothesis and we also need to consider the supposition, say, $x\geq y\geq z\geq 0$, of the proof. Hence, we need to find a way to combine some cases to get a concise proof. Am I correct?

user547265
  • 443

2 Answers2

1

You seem to want to show the implication that if $x^t(x-y)(x-z) + y^t(y-z)(y-x)+z^t(z-x)(z-y)=0$ for $x, y, z \geqslant 0$ and $t>0$ then at least two among $x, y, z$ are the same and the other zero, or all are equal.

First suppose all are distinct, i.e. WLOG $x>y> z\geqslant 0$ using symmetry. Then we may divide throughout by the positive number $(x-y)(y-z)(x-z)$ to get $$\frac{x^t}{y-z}+\frac{z^t}{x-y}=\frac{y^t}{x-z}$$ Note that all the three fractions are necessarily non-negative. Further, $x^t> y^t$ and $y-z < x-z$, so the first term on LHS is strictly higher than the RHS. Hence this equality is not possible, i.e. $x, y, z$ cannot be distinct.

Now we consider that perhaps two among the three are equal, i.e. $y=z$, say. In this case the equality becomes $x^t(x-y)^2=0$, which is satisfied iff $x=0$ or $x=y$.

Hence we have proved the implication required.

Macavity
  • 48,039
  • PS: the same argument works with a little tweak for $x,y,z$ real when $t$ Is even and positive or if $x^t$ is replaced by some increasing function $f(t)$ etc. – Macavity Jun 14 '18 at 07:08
0

The equality case in the Schur's inequality follows from the proof.

For example, let $t>0$ and $x$, $y$ and $z$ are non-negatives.

Since our inequality is symmetric, we can assume $x\geq y\geq z$.

Thus, $$\sum_{cyc}x^t(x-y)(x-z)\geq x^t(x-y)(x-z)+y^t(y-x)(y-z)=$$ $$=(x-y)(x^t(x-z)-y^t(y-z))\geq0.$$ The equality occurs for $$z^t(z-x)(z-y)=0$$ and for $$(x-y)(x^t(x-z)-y^t(y-z))=0.$$ Now, easy to see that the equality occurs for $x=y=z$ or for $x=y$, $z=0$ and for cyclic permutations of the last.

Michael Rozenberg
  • 203,855
  • Why do we say the equality occurs for $z^t(z-x)(z-y)=0$ and for $(x-y)(x^t(x-z)-y^t(y-z))=0$ instead of saying the equality occurs for $z^t(z-x)(z-y)=-1$ and $(x-y)(x^t(x-z)-y^t(y-z))=1$, or saying they equal some other additive inverses? Can we prove the case of equality from the equation $(x-y)(x^t(x-z)-y^t(y-z)) +z^t(z-x)(z-y) = 0$? – user547265 Jun 14 '18 at 04:50
  • @user547265 In my solution there are number of steps. The first step is: Let $x\geq y\geq z$. Is it clear? – Michael Rozenberg Jun 14 '18 at 06:30