$S^1-\{p\}$ is homeomorphic to $\mathbb{R}$

Question

$S^1-\{p\}$ is homeomorphic to $\mathbb{R}$, drawing the picture I understand but I find difficulty in finding map. Please help . Thanks

Answer 1

Just consider the homeomorphism from $\mathbb R$ onto $S^1\setminus\{(-1,0)\}$ define by$$x\mapsto\left(\frac{1-x^2}{1+x^2},\frac{2x}{1+x^2}\right).$$

Answer 2

You can write the required homomorphism as the composition of two functions: $$t\longmapsto(\cos t,\sin t),\qquad t\in(-\pi,\pi)$$ and $$x\longmapsto 2\arctan x,\qquad x\in\Bbb R.$$

Answer 3

This homeomorphism can be seen as the $v={}$central projection from $P$ onto the $x$-axis: 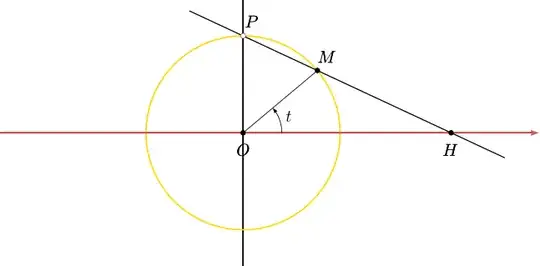Now the equation of line $(PH)$ is $\;\dfrac x1+\dfrac y{x_H}=1$. As it passes through $M(\cos t,\sin t)$, we have $$\cos t+\frac{\sin t}{x_H}=1,\quad\text{whence }\quad x_H=\frac{\sin t}{1-\cos t}.$$

Answer 4

Let $\ell$ be a line parallel to the tangent line to $S^1$ at $p.$ A line through $p$ other than the tangent line intersects $S^1$ once and intersects $\ell$ once. That's a homeomorphism.