Showing that stereographic projection is a homeomorphism

Question

For any $n\geq 0$, the unit $n$-sphere is the space $S^{n}\subset \mathbb{R}^{n+1}$ defined by $$ S^{n}=S^{n}(1) := \left\{ (x_{1}, \dots, x_{n+1}) \;\middle\vert\; \sum_{i=1}^{n+1} x_{i}^{2} = 1 \right\} $$ with the subspace topology. The point $P = (0, \dots, 0, 1)$ in $S^{n}$ called the north pole. Then we have the following conclusion:

$\qquad\qquad\qquad$ For any $n\geq 0$, $S^{n}$ with the north pole removed is homeomorphic to $\mathbb{R}^{n}$.

---

$\qquad\qquad\qquad\qquad\qquad$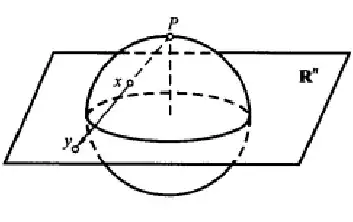

From FIGURE 1-1 ,we define a map $$ f: S^{n} \setminus \{P\} \to \mathbb{R}^{n}, \quad x \mapsto \frac{1}{1-x_{n+1}} \cdot (x_1, \cdots , x_n). $$

(This map is called stereographic projection.)

It can be described geometrically as follows: Given a point $x = (x_{1}, \dots, x_{n+1}) \in S^{n} \setminus \{P\}$, stereographic projection sets $f(x) = y$, where $(y, 0)$ is the point where the line through $P$ and $x$ meets the subspace $\mathbb{R}^{n} \times \{0\}$ at $u = (y,0) = (y_{1}, \dots, y_{n}, y_{n+1})$.

Hence,
$$ \left\{\begin{matrix} u = \lambda x+(1-\lambda )P \\ y_{n+1} = 0 \end{matrix}\right. \quad(\lambda \in\mathbb{R}) \Longrightarrow \lambda = \frac{1}{1-{x}_{n+1}}. $$ So the analytical expression of the stereographic projection is $$ f(x_{1}, \dots, x_{n+1}) = \left( \frac{x_{1}}{1-{x}_{n+1}}, \dots, \frac{x_{n}}{1-{x}_{n+1}} \right) \in \mathbb{R}^{n}. $$

---

From the geometric intuition,we can get the map $f: S^{n} \setminus \{P\} \to \mathbb{R}^{n}$ is bijective, but how can I prove it theoretically. Further, I need some rigorous proofs that $f: S^{n} \setminus \{P\} \to \mathbb{R}^{n}$ is a homeomorphism. (We must strictly demonstrate that $f$ is injective, surjective, and continuous.)

Another question:

I know the analytical expression of the inverse $f^{-1}: \mathbb{R}^{n} \to S^{n} \setminus \{P\}$ is $$ f^{-1} (y_1, \dots, y_n) = \frac{1}{\|y\|^2 + 1}(2y_1, \dots, 2y_n, \|y\|^2 - 1), \quad \text{where } \|y\|^2 = y_1^2 + \dots + y_n^2. $$ But how can I get this expression?

Who can provide some related materials or solutions about these? (I want use some knowledge of Differential Calculus in Several Variables to solve these questions). Any of your help will be appreciated!

Answer 1

Hint: To show that $f$ is bijective, one can often (as can be managed here) compute $f^{-1}$ explicitly. Then, to show that $f$ is a homeomorphism, by definition it remains to show that $f$ and $f^{-1}$ are continuous, but they are both visibly compositions of continuous functions.

Answer 2

Alternatively, stereographic projection maps circles to circles, and so for topological reasons $f$ maps open disks in the planes into open discs on $S^n - \{p\}$ (regions with circular boundary). But the set of open disks in the plane is a basis for the standard topology on the plane, and hence (once you know it exists) $f^{-1}$ is continuous. Similarly, so is $f$.

Answer 3

Let $x=(x_1,\ldots,x_n,x_{n+1})$ be the point in the sphere whose projection on the plane is $y = (y_1,\ldots,y_n)$. As you said before, the relation between the coordinates of those points is: \begin{equation} y_i = \frac{x_i}{1-x_{n+1}} \quad \forall i \in \{ 1,\ldots, n \}, \end{equation} with $y_{n+1} = 0$. We want to find the inverse of the projection, $f^{-1}: \mathbb{R}^n \longrightarrow \mathbb{S}^n-\{p\}$, i.e. we want to find $x_i$ as a function of $y_i$, given $y_i$. But the above relation only gives us $n$ equations and we have $n+1$ unknowns. To find one more equation, we can do some reverse-engineering. For $f^{-1}$ to be well defined, it is necessary that the output be a point of the sphere. This gives us the extra equation we needed: $$ x_1^2 + \ldots + x_n^2 + x_{n+1}^2 = 1.$$ Plugging in the above relations: $$ 1 = (1-x_{n+1})^2(y_1^2+\ldots + y_n^2) + x_{n+1}^2 = (1-x_{n+1})^2||y||^2 + x_{n+1}^2.$$ Equivalently, this is a second order equation with $x_{n+1}$ being the only unknown: $$ (1-||y||^2)x_{n+1}^2 -2||y||^2x_{n+1} + (||y||^2-1) = 0.$$ If you apply the classical formula to solve this equation, you either get $x_{n+1} = 1$ or $x_{n+1} = 1 - 2/(1+||y||^2)$. Since we know that $x_{n+1}$ must satisfy the initial relations, it is obvious that the first solution must be discarded, so $x_{n+1} = 1 - 2/(1+||y||^2)$. Plugging this in the initial equations, we get: $$ x_i = \frac{2y_i}{1+||y||^2} \quad \forall i \in \{ 1,\ldots, n \},$$ $$ x_{n+1} = 1 - \frac{2}{1+||y||^2} = \frac{||y||^2-1}{1+||y||^2}. $$

Answer 4

You are asking two questions in your post: i) How to prove that $f\circ f^{-1} = f^{-1}\circ f = \text{Id}$ and bicontinuity, ii) how to obtain the expression for the inverse?

ii) I myself tried to do this geometrically, but at least I haven't managed to do so. My best guess would be: Take $n = 2$ or $n = 3$, do it analytically there and then generalize to an arbitrary number of dimensions. Once you have it, you can explicitly show i). Or maybe one can even take the general definition of the stereographic projection and invert it in general...

i) Concerning the bicontinuity, I refer to this post and the already given answers.

• Let's first prove that $f(f^{-1}(x)) = x$, where $x \in \mathbb R^{n}$. This one is straightforward: $$ f(f^{-1}(x)) = f\left( \left( \frac{2x_1}{1+||x||_2^2}, \dots, \frac{2x_n}{1+||x||_2^2}, 1-\frac{2}{1+||x||_2^2} \right)^T \right) = \dots = x.$$ Again, this one is straightforward, just use the stereographic map $f$.

• Now let's prove that $f^{-1}(f(x))$, where $x\in S^n\backslash\{p\}\subset\mathbb R^{n+1}$: $$f^{-1}(f(x)) = f^{-1}\left(\frac{1}{1-x_{n+1}} \begin{pmatrix}x_1, \dots, x_n\end{pmatrix}^T \right)$$

I will prove $f^{-1}\left( \frac{1}{1-x_{n+1}}\begin{pmatrix}x_1, \dots, x_n\end{pmatrix}^T\right) = x$ by proving $f^{-1}(\dots)_i = x_i$, where I denote by $f^{-1}(\dots)_i$ the $i$-th component of $f^{-1}(\dots)$ for $i\in \{1, \dots, n-1\}$, and by separately proving $f^{-1}(\dots)_n = x_n$. I do this because of the way that $f^{-1}$ is given: The last component of the input is transformed differently than the other components.

So, let's start with $f^{-1}(f(x))_i$: $$f^{-1}(f(x))_i = \frac{2x_i}{1-x_{n+1}}\cdot \frac{1}{1+\lvert\lvert \frac{1}{1-x_{n+1}}\begin{pmatrix}x_1, \dots, x_{n+1}\end{pmatrix}^T \rvert\rvert_2^2} = \frac{2x_i}{1-x_{n+1}+\frac{1}{1-x_{n+1}}\sum_{j=1}^{n}x_j^2}.$$ We can now use two facts: Firstly, $\lvert\lvert x \rvert\rvert_2^2 = \sum_{j=1}^{n}x_j^2 + x_{n+1}^2$, since $x\in S^n\backslash \{p\}\subset \mathbb R^{n+1}$. Secondly, $\lvert\lvert x \rvert\rvert_2^2 = 1$, by definition of the unit ball. Thus, we can rewrite $\sum_{j=1}^{n}x_j^2 = 1-x_{n+1}^2$: $$ f^{-1}(f(x))_i = \frac{2x_i}{1-x_{n+1}+\frac{1-x_{n+1}^2}{1-x_{n+1}}} = \dots = x_i,$$ which is now easy to show. Similarly, we can show that $f^{-1}(f(x))_n = x_n$. $\blacksquare$