For $a\in\mathbb N$, let $R_a\subseteq\mathbb{R}$ be the set of real roots of polynomials whose coefficients are integers with absolute value at most $a$.
$$R_a=\left\{r\in\mathbb{R}\middle|\sum_{i=0}^na_ir^i=0,n\in\mathbb N,a_i\in\mathbb Z,|a_i|\leq a, a_n\neq 0\right\}$$
(Note that the degrees of the allowed polynomials aren't bounded.)
I want to know which numbers can be arbitrarily well approximated by such roots. In particular, is $R_a$ dense on some interval for any $a$?
Discussion:
If $r\in R_a$ and $r\neq 0$ then $1/r\in R_a$, since by reversing the order of the coefficients of the polynomial of which $r$ was a root one obtains a polynomial of which $1/r$ is a root.
In the comments, mathworker21 noted that by considering the polynomial $1 - aX -\dots-aX^n$ one can show that every nonzero $r\in R_a$ satisfies $|r|>\frac{1}{a+1}$. Therefore we also have $|r|<a+1$, so $R_a$ is bounded.
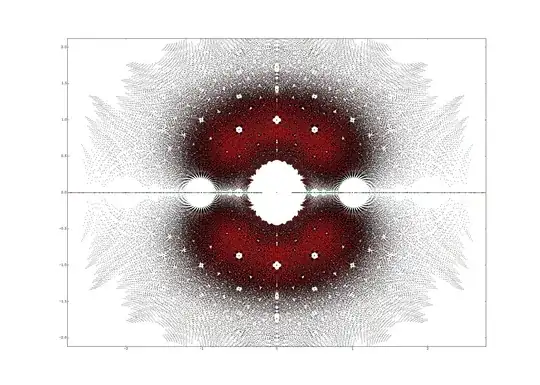
We could also ask about the set $R_a^\mathbb C$ of the roots of such polynomials in $\mathbb C$. John Baez has a page about such sets here, which contains some beautiful pictures.
He's also written a paper, which gives a reference to a paper by Thierry Bousch in which it is proved that the roots of the Littlewood polynomials (those with coefficients $\pm1$ only) are dense on the annulus $2^{-1/4}<|z|<2^{1/4}$.
Since $\{-1,1\}\subseteq\{-1,0,1\}$, this answers the complex analogue of my question: the set $R_1^\mathbb C$ is dense on some ball. Unfortunately the paper is written in French, so I can't tell if the proof generalises to the reals. (The real result isn't an immediate corollary of the complex version, because there might be a sequence in $R_a^\mathbb C$ tending to $x\in\mathbb R$ without there being such a sequence in $R_a^\mathbb C\cap\mathbb R$.)