Using the unisolvent method to find the shape functions for a regular unit hexagon with vertices: $\{x,y\}=\{(1,0),(\frac{1}{2},\frac{\sqrt{3}}{2})(-\frac{1}{2},\frac{\sqrt{3}}{2}),(-1,0),(-\frac{1}{2},-\frac{\sqrt{3}}{2}),(\frac{1}{2}, -\frac{\sqrt{3}}{2}\}$,
using a quadratic polynomial basis for the approximation.
Can you give me a hint for this case? By trying to solve it, the matrix $A$ resultet singular.
Taking the hexagon as a parent element gives rise to the following matrix: $$ A = \begin{bmatrix} 1 & x_1 & y_1 & x_1 y_1 & x_1^2 & y_1^2 \\ 1 & x_2 & y_2 & x_2 y_2 & x_2^2 & y_2^2 \\ 1 & x_3 & y_3 & x_3 y_3 & x_3^2 & y_3^2 \\ 1 & x_4 & y_4 & x_4 y_4 & x_4^2 & y_4^2 \\ 1 & x_5 & y_5 & x_5 y_5 & x_5^2 & y_5^2 \\ 1 & x_6 & y_6 & x_6 y_6 & x_6^2 & y_6^2 \end{bmatrix} = \begin{bmatrix} 1 & 1 & 0 & 0 & 1 & 0 \\ 1 & 1/2 & \sqrt{3}/2 & \sqrt{3}/4 & 1/4 & 3/4 \\ 1 & -1/2 & \sqrt{3}/2 & -\sqrt{3}/4 & 1/4 & 3/4 \\ 1 & -1 & 0 & 0 & 1 & 0 \\ 1 & -1/2 & -\sqrt{3}/2 & \sqrt{3}/4 & 1/4 & 3/4 \\ 1 & 1/2 & -\sqrt{3}/2 & -\sqrt{3}/4 & 1/4 & 3/4 \end{bmatrix} $$ And indeed, upon trying to determine the inverse, MAPLE says:
> inverse(A); Error, (in linalg[inverse]) singular matrix
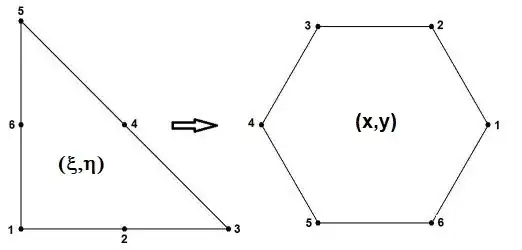
Introducing local coordinates $(\xi,\eta)$ instead of the global coordinates $(x,y)$ and taking a six node triangle as the parent element gives rise to the following. For an arbitrary function $f$ at the element we now have: $$ f = a_1+a_2\xi+a_3\eta+a_4\xi\eta+a_5\xi^2+a_6\eta^2 \quad \Longrightarrow \\ \begin{bmatrix} f_1 \\ f_2 \\ f_3 \\ f_4 \\ f_5 \\ f_6 \end{bmatrix} = \begin{bmatrix} 1 & \xi_1 & \eta_1 & \xi_1 \eta_1 & \xi_1^2 & \eta_1^2 \\ 1 & \xi_2 & \eta_2 & \xi_2 \eta_2 & \xi_2^2 & \eta_2^2 \\ 1 & \xi_3 & \eta_3 & \xi_3 \eta_3 & \xi_3^2 & \eta_3^2 \\ 1 & \xi_4 & \eta_4 & \xi_4 \eta_4 & \xi_4^2 & \eta_4^2 \\ 1 & \xi_5 & \eta_5 & \xi_5 \eta_5 & \xi_5^2 & \eta_5^2 \\ 1 & \xi_6 & \eta_6 & \xi_6 \eta_6 & \xi_6^2 & \eta_6^2 \end{bmatrix} \begin{bmatrix} a_1 \\ a_2 \\ a_3 \\ a_4 \\ a_5 \\ a_6 \end{bmatrix} = A \begin{bmatrix} a_1 \\ a_2 \\ a_3 \\ a_4 \\ a_5 \\ a_6 \end{bmatrix} $$ Where: $$ A = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 \\ 1 & 1/2 & 0 & 0 & 1/4 & 0 \\ 1 & 1 & 0 & 0 & 1 & 0 \\ 1 & 1/2 & 1/2 & 1/4 & 1/4 & 1/4\\ 1 & 0 & 1 & 0 & 0 & 1 \\ 1 & 0 & 1/2 & 0 & 0 & 1/4 \end{bmatrix} \quad \Longrightarrow \\ A^{-1} = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 \\ -3 & 4 & -1 & 0 & 0 & 0 \\ -3 & 0 & 0 & 0 & -1 & 4 \\ 4 & -4 & 0 & 4 & 0 & -4 \\ 2 & -4 & 2 & 0 & 0 & 0 \\ 2 & 0 & 0 & 0 & 2 & -4 \end{bmatrix} \quad \Longrightarrow \quad \begin{bmatrix} a_1 \\ a_2 \\ a_3 \\ a_4 \\ a_5 \\ a_6 \end{bmatrix} = A^{-1} \begin{bmatrix} f_1 \\ f_2 \\ f_3 \\ f_4 \\ f_5 \\ f_6 \end{bmatrix} $$ Giving difference schemes for the coefficients $a$ : $$ \begin{cases} a_1 = f_1 \\ a_2 = -3f_1+4f_2-f_3 \\ a_3 = -3f_1-f_5+4f_6 \\ a_4 = 4f_1-4f_2+4f_4-4f_6 \\ a_5 = 2f_1-4f_2+2f_3 \\ a_6 = 2f_1+2f_5-4f_6 \end{cases} $$ But the result can be grouped in another way: $$ f = \begin{bmatrix} a_1 & a_2 & a_3 & a_4 & a_5 & a_6 \end{bmatrix} \begin{bmatrix} 1 \\ \xi \\ \eta \\ \xi\eta \\ \xi^2 \\ \eta^2 \end{bmatrix} \\ = \begin{bmatrix} f_1 & f_2 & f_3 & f_4 & f_5 & f_6 \end{bmatrix} \left( A^{-T} \begin{bmatrix} 1 \\ \xi \\ \eta \\ \xi\eta \\ \xi^2 \\ \eta^2 \end{bmatrix} \right) \\ = N_1f_1+N_2f_2+N_3f_3+N_4f_4+N_5f_5+N_6f_6 $$ Where $N$ are the shape functions at the element: $$ \begin{cases} N_1 = 1-3\xi-3\eta+4\xi\eta+2\xi^2+2\eta^2 \\ N_2 = 4\xi-4\xi\eta-4\xi^2 \\ N_3 = -\xi+2\xi^2 \\ N_4 = 4\xi\eta \\ N_5 = -\eta+2\eta^2 \\ N_6 = 4\eta-4\xi\eta-4\eta^2 \end{cases} $$ As every function, the global coordinates can be expressed into the local coordinates. Let's just do it for our hexagon: $$ \begin{cases} x = N_1x_1+N_2x_2+N_3x_3+N_4x_4+N_5x_5+N_6x_6 \\ y = N_1y_1+N_2y_2+N_3y_3+N_4y_4+N_5y_5+N_6y_6 \end{cases} \quad \Longrightarrow \\ \begin{cases} x = 1 - \xi/2 - \eta/2 - 4\xi\eta - \xi^2 - \eta^2 \\ y = \sqrt{3}/2\left(3\xi-2\xi^2-3\eta+2\eta^2\right) \end{cases} $$ Combined with $\;f=N_1f_1+N_2f_2+N_3f_3+N_4f_4+N_5f_5+N_6f_6\;$ all function behaviour at the hexagon is determined. However, solving $(\xi,\eta)$ from the equations for $(x,y)$ is not an easy exercise. It may be questioned if the mapping $\,(\xi,\eta)\to(x,y)\,$ is unique. Quite fortunately, for our hexagon, such seems to be the case:
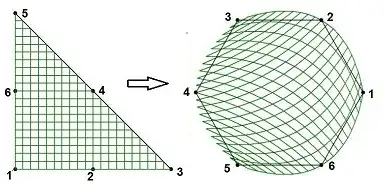
Can we understand what's going on in that picture? It is claimed, for example, that the boundary of the mapping in the $(x,y)$ plane is not a circle, but a piecewise continuous parabola around the hexagon: $$ 1-2-3: \qquad \eta = 0 \quad \Longrightarrow \quad \begin{cases} x = 1-\xi/2-\xi^2 \\ y = \sqrt{3}/2\left(3\xi-2\xi^2\right) \end{cases} \\ 3-4-5: \qquad \eta = 1-\xi \quad \Longrightarrow \quad \begin{cases} x = -1/2-2\xi+2\xi^2 \\ y = \sqrt{3}/2\left(2\xi-1\right) \end{cases} \\ 5-6-1: \qquad \xi = 0 \quad \Longrightarrow \quad \begin{cases} x = 1-\eta/2-\eta^2 \\ y = \sqrt{3}/2\left(-3\eta+2\eta^2\right) \end{cases} $$
In this case, when the matrice $L$ is singular, we can always choose a higher polynomial. For this, we need also additional nodes, which can be side nodes or interior nodes. Pascal triangle is a good scheme of choosing these points.