Orthogonal Projection Area of a 3-d Cube

Question

If you're given a 3-d cube centered at the origin, i.e. the center of the cube is at $(0,0,0)$. If you rotate the cube in $x$, $y$, and $z$ direction, then how can you find the area of its orthogonal projection. For example, if you don't rotate the cube at all, then the area is just $1$. However, say you rotate the cube $45^\circ$ along the line $x=y=0$, then the area comes out to $\sqrt{2}\cdot 1 = \sqrt{2}$. Is there a general formula for this where you're given some rotation and you have to find the orthogonal projected area? What about the other way, i.e. if you're given the area, can you find the coordinates of the cube (more interested in this case)?

I think this may be related to my question: Width of a tilted cube But, instead of width, I'm working with area.

Answer 1

To make the calculations simpler , let's place the unit cube with one vertex at the origin and the edges along the axes, so that its vertices are $(0,0,0),(1,0,0),\cdots (1,1,1)$.

Then, let' s rotate the cube. We consider the axis $z$ as the projection direction, and the plane $x,y$ as the projection plane.
The rotation around the $z$ axis will only produce a rotation of the projected shape, so can omit that and consider only the rotation around $x$ by an angle $\alpha$ and around $y$ by an angle $\beta$.
Due to symmetry we can limit the range to $[0,\pi/4]$ for both the angles.

The matrices
$$ {\bf R}_{\,{\bf x}} (\alpha ) = \left( {\matrix{ 1 & 0 & 0 \cr 0 & {\cos \alpha } & { - \sin \alpha } \cr 0 & {\sin \alpha } & {\cos \alpha } \cr } } \right)\quad {\bf R}_{\,{\bf y}} (\beta ) = \left( {\matrix{ {\cos \beta } & 0 & {\sin \beta } \cr 0 & 1 & 0 \cr { - \sin \beta } & 0 & {\cos \beta } \cr } } \right) $$
when applied to the original cube vertices will give the coordinates of the rotated ones,
expressed in the base system. The rotation angle is according to the Right Hand rule.

For a rotation in the range above, the six "prominent" vertices defining the projection (see the sketch above) will be
the column vectors of the following matrix
$$ \left( {\matrix{ 0 & 0 & 0 & 1 & 1 & 1 \cr 0 & 1 & 1 & 0 & 0 & 1 \cr 1 & 1 & 0 & 1 & 0 & 0 \cr } } \right) $$

We multiply then the six vectors (i.e. the whole matrix above) by ${\bf R}_{\,{\bf x}} (\alpha ){\bf R}_{\,{\bf y}} (\beta )$.
Inverting the multiplication order will just lead to an exchange between $\alpha$ and $\beta$ in following results.

On the vectors obtained, we put to zero the $z$ component to obtain the projection on the $x,y$ plane.
Actually, we have better put it to $1$ so to get the points in homogeneous coordinates and calculate the area
by taking the determinant. Let's indicate such vectors as $\bf u_1,\cdots,\bf u_6$.
Then, looking at the sketch, the Area will be given by the sum of the two determinants
$$ \eqalign{ & A = \left| {\left( {\matrix{ {{\bf u}_{\,1} } & {{\bf u}_{\,2} } & {{\bf u}_{\,3} } \cr } } \right)} \right| - \left| {\left( {\matrix{ {{\bf u}_{\,1} } & {{\bf u}_{\,3} } & {{\bf u}_{\,4} } \cr } } \right)} \right| = \cr & = \sin \alpha + \cos \alpha \left( {\cos \beta + \sin \beta } \right) = \cr & = \sin \alpha + {{\sqrt 2 } }\cos \alpha \cos \left( {\beta - \pi /4} \right) \cr} $$
where the minus sign in front of the second determinant is to render it positive in the considered range
for the angles.

A graph of $A(\alpha,\beta)$ is given below.

$A$ attains its maximum $=\sqrt{3}$ at $\beta = \pi/4,\; \alpha = \arctan(\sqrt{2} /2) \approx {35.26}^\circ$.

Then the problem you are posing, of finding the angles of rotation given $ 1 \le A \le \sqrt{3}$, in general has multiple solutions, that can be found by solving the identity above, upon fixing an appropriate value of $\alpha$ or $\beta$.

Answer 2

Now that the Code Jam Qualifiers are over, I'll post a full solution.

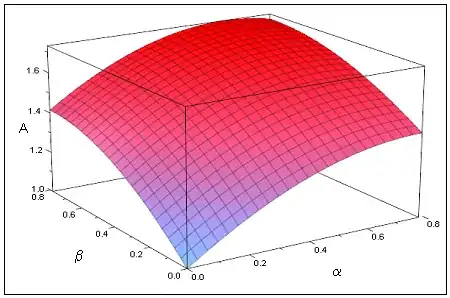
First, we know that the minimum possible area is $1$, which is the area of a single face. The maximal area is $\sqrt{3}$, which is given in the problem as the upper limit for full points $-$ written as the inequality $1.000000<A<1.732050$. You can also see why this is the maximum by checking out the answer G Cab provided.

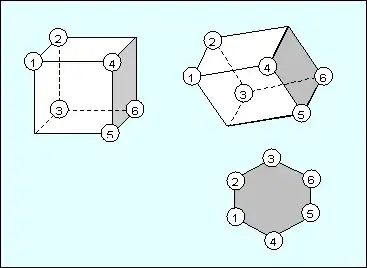
First, we'll need a way to calculate the area of a projected cube as a function of it's normal vectors. We let $n_1=(n_{11},n_{12},n_{13}),n_2=(n_{21},n_{22},n_{23}),n_3=(n_{31},n_{32},n_{33})$ be the vectors pointing from the center of the cube to the center point of 3 nonparallel faces, and $n_p = (0,1,0)$ be the normal vector of the plane. Then, if $\phi_i$ is the angle between $n_i$ and $n_p$, the area of the projection is $A = \sum_{i=1}^3 |\cos\phi_i|$. We can calculate $|\cos\phi_i| =\left|\frac{n_i\cdot n_p}{|n_i||n_p|}\right| = 2|n_{i2}|$, since $|n_i|=\frac{1}{2}$. This gives us the formula for the area $A = 2\sum_{i=1}^3 |n_{i2}| = 2|n_{12}|+2|n_{22}|+2|n_{32}|$.

Next, we need to find a configuration which gives the minimum possible area and one which gives the maximum. The minimum area is easy, as it's the default state of the cube. If we write the coordinates as a matrix $N = (n_{ij})$, we can see that a minimal configuration is

$\frac{1}{2}I_3 = \begin{bmatrix}1/2&0&0\\ 0&1/2&0\\ 0&0&1/2\end{bmatrix}$,

and the area is twice the sum of the second row: $A = 2(0+1/2+0) = 1$. A maximal configuration can be found when the long diagonal of the cube (from bottom left front to top right back) is parallel to $n_p$. To show this, we will look at it from a different coordinate system, where the cube is aligned with the axes, with normal vectors $m_i=\frac{1}{2}e_i$, and the plane normal vector is $m_p = \left(\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}}\right)$. This this configuration, the cosine of the angles between the cube normals and plane normal are $\cos\theta_i = \frac{1}{\sqrt{3}}$, so the area is $A=\sqrt{3}$, which is known to be the maximum.

So, now that we have a minimum configuration and a maximum configuration, if we can generate a continuous function between these two orientations, then Intermediate Value Theorem will guarantee that there's a solution to the function for any possible $A$. To do this, we take an axis of rotation to be the line $x=z, y=0$, which is written as $(\frac{1}{\sqrt{2}},0,\frac{1}{\sqrt{2}})$ in vector form. Let $\psi$ be the angle in radians rotated about this axis from the starting minimal configuration. Then, $A = f(\psi)$ has $f(0) = 1$. Further, if we rotate by some amount $\psi_m$, we will reach the maximal configuration, so $f(\psi_m) = \sqrt{3}$.

To calculate $f(\psi)$, we use the same formula for calculating the area of the projection, but we multiply each of the $n_i$ by the corresponding rotation matrix $R = \begin{bmatrix}\frac{1+\cos\psi}{2} & -\frac{\sin\psi}{\sqrt{2}} & \frac{1-\cos\psi}{2}\\ \frac{\sin\psi}{\sqrt{2}} & \cos\psi & -\frac{\sin\psi}{\sqrt{2}} \\ \frac{1-\cos\psi}{2} & -\frac{\sin\psi}{\sqrt{2}} & \frac{1+\cos\psi}{2} \end{bmatrix} $.

This gives $N = R(\frac{1}{2}I_3) = \frac{1}{2}R$, and summing the absolute values of the second row gives the area as $A = |\cos\psi|+\sqrt{2}|\sin\psi|$. For $0 < \psi < \pi/2$, we can drop the absolute values, so that $A = f(\psi) = \cos\psi + \sqrt{2}\sin\psi$. This function takes it's first maximum at $\psi_m = 2\tan^{-1}\left(\frac{\sqrt{2}}{1+\sqrt{3}}\right) \approx 0.95532 < \pi/2$. So, for a given $A$, we can find $\psi_A = 2\tan^{-1}\left(\frac{\sqrt{2}-\sqrt{3-A^2}}{1+A}\right)$. This gives us (with a little bit of trigonometry) $\cos\psi = \frac{1}{3}(A+\sqrt{2}\sqrt{3-A^2})$ and $\sin\psi = \frac{1}{3}(\sqrt{2}A-\sqrt{3-A^2})$.

Last, all we need to do is substitute these values into the matrix $N$ to get the final answer:

$N = \begin{bmatrix}\frac{1}{12}(3+A+\sqrt{6-2A^2}) & \frac{1}{12}(-2A+\sqrt{6-2A^2}) & \frac{1}{12}(3-A-\sqrt{6-2A^2}) \\ \frac{1}{12}(2A-\sqrt{6-2A^2}) & \frac{1}{6}(A+\sqrt{6-2A^2}) & \frac{1}{12}(-2A+\sqrt{6-2A^2}) \\ \frac{1}{12}(3-A-\sqrt{6-2A^2}) & \frac{1}{12}(2A-\sqrt{6-2A^2}) & \frac{1}{12}(3+A+\sqrt{6-2A^2}) \end{bmatrix}$,

where the columns are the coordinates of the points in the center of 3 nonparallel faces.

Answer 3

If you consider a rotation in the same axis as one of the faces (I'm not sure how to word this well), so that the projection is always a rectangle (NOT a hexagon), then the projection's area will be w*d. Where w is the width of the cube and d is the orthogonal projection of the diagonal across the tilted face. For a unit-cube, this can be written nicely as

$$ A = \sqrt2cos(\theta) $$

You can use matrix transformations to find coordinates of the cube using your angle.

PS: this will only help for test set 1 of the codejam problem

Answer 4

It happens that the area of the projection of a unit cube into a plane is numerically equal to the length of the projection on the orthogonal line.

Reference: https://londmathsoc.onlinelibrary.wiley.com/doi/abs/10.1112/blms/16.3.278

This fact can simplify the problem since we know that the minimum shadow is given by the height of the cube, which is 1. And the maximum is given by the length of its diagonal which is $\sqrt 3$. If we start with an horizontal cube with the diagonal on the $xz$-plane we can rotate in the $xz$ plane so that the height of the cube is equal to the z coordinate of the rotated diagonal and can hence be easily computed.

To be more precise, suppose the cube has the edges parallel to the coordinate axes. First we rotate it in the $xy$-plane so that the diagonal goes into the plane $y=0$. To achieve this we need to apply this rotation matrix: $$ R = \begin{pmatrix} \sqrt 2 /2 & \sqrt 2/2 & 0 \\ -\sqrt 2 /2 & \sqrt 2/2 & 0 \\ 0 & 0 & 1 \end{pmatrix}. $$ Then we apply the rotation of an angle $\theta$ around the $y$ axis: $$ T_\theta = \begin{pmatrix} \cos \theta & 0 & -\sin\theta \\ 0 & 1 & 0 \\ \sin \theta & 0 & \cos \theta \end{pmatrix}. $$

The area of the projection should be equal to the $z$ coordinate of the rotated diagonal. So it should be: $$ (0,0,1)\cdot T_\theta \cdot R \cdot \begin{pmatrix}1\\1\\1\end{pmatrix} $$ while the coordinates of the center of the faces (as requested in the codejam problem) can be easily computed by appling $T_\theta R$ to the original coordinates which are (for a unit cube centered in the origin): $$ T_\theta R \begin{pmatrix}1/2 \\ 0 \\ 0\end{pmatrix} \qquad T_\theta R \begin{pmatrix}0 \\ 1/2 \\ 0\end{pmatrix} \qquad T_\theta R \begin{pmatrix}0 \\ 0 \\ 1/2 \end{pmatrix}. $$

Answer 5

The image of each cube’s face is a parallelogram, possibly one that has collapsed to a line segment. Since the projection is orthogonal, the image plane can be translated without affecting the size or shape of the cube’s image. Assume for now that it’s positioned so that it doesn’t intersect the cube. I won’t prove it formally here, but a bit of thought and visualization should convince you that the shadow of the cube is the union of the images of the three faces nearest the image plane, i.e., the three faces that meet at the vertex nearest the image plane. If there are two equidistant vertices, we can choose either because the faces that aren’t common to both of them are orthogonal to the image plane, and similarly when there are four equidistant vertices—only their common face contributes to the shadow area. These three parallelograms intersect only along their edges, so the area of the shadow is just the sum of the areas of these parallelograms. The images of opposite faces are congruent, so we don’t really need to figure out which vertex is closest to the image plane. We can choose any three faces that meet at a common vertex and sum the areas of their images to get the total shadow area.

To make the computations simpler, we can rotate the image plane instead of rotating the cube. Let $\mathbf n$ be a unit normal of the image plane, which we now take to be passing through the origin. The size and shape of the image are also unaffected by translations of the cube, so w.l.o.g. we place it so that it has a vertex at the origin and lies within the first octant. We can also w.l.o.g. assume a unit cube. All of the transformations involved are linear, so the unit cube shadow area need only be scaled by the square of the side length to get the actual area.

The orthogonal projection of a vector $\mathbf v$ onto the image plane is its orthogonal rejection from $\mathbf n$: $$P\mathbf v = \mathbf v - (\mathbf n^T\mathbf v)\mathbf n = (I-\mathbf n\mathbf n^T)\mathbf v.$$ The standard basis vectors $\mathbf i$, $\mathbf j$ and $\mathbf k$ are three edges of the cube that share a vertex and the areas of the images of the faces they define are the norms of the pairwise cross products of $P\mathbf i$, $P\mathbf j$, $P\mathbf k$. Taking the first two, we have $$\|P\mathbf i\times P\mathbf j\| = \|\operatorname{cof}(P)(\mathbf i\times\mathbf j)\| = \|\operatorname{cof}(P)\mathbf k\| = \|(I-P)\mathbf k\| = |n_z| $$ and similarly for the other two faces. (One could also argue that planar objects are foreshortened by a factor equal to the cosine of the dihedral angle.) Therefore, the area of the unit cube’s shadow is equal to $|n_x|+|n_y|+|n_z|$ and the area of the shadow of a cube with side length $s$ is $$s^2(|n_x|+|n_y|+|n_z|).$$ This expression is symmetric in the three components of $\mathbf n$, so it will be maximal when $n_x=n_y=n_z=\pm\frac1{\sqrt3}$.

Going back to the original problem in which the cube is rotated, you haven’t specified the image plane in your question. Let’s assume that it’s the $x$-$y$ plane, which has normal $\mathbf k$. Rotating the cube is equivalent to applying the inverse rotation to the image plane normal, so our rotated normal $\mathbf n$ is the last row of the cube rotation matrix.

To go from a given shadow area $A\in[1,\sqrt3]$ to a rotation that produces that area, it’s clear from the above that you can choose any unit vector $\mathbf n$ with $|n_x|+|n_y|+|n_z|=A$ and $n_x^2+n_y^2+n_z^2=1$. That is, $\mathbf n$ lies on the intersections of the unit sphere with the eight planes $\pm x\pm y\pm z=A$. These planes are at a distance of $\frac1{\sqrt3}A$ from the origin, so the intersections are circles with radius $r=\sqrt{1-\frac13A^2}$. By symmetry, we can stick to the first octant, and a not-unreasonable choice there is $$\mathbf n(A) = \frac A3(1,1,1)+\frac r{\sqrt6}(-1,-1,2) = \frac16\left(2A-\sqrt{6-2A^2},2A-\sqrt{6-2A^2},2A+2\sqrt{6-2A^2}\right),$$ which is closest to the $z$-axis. Having fixed $\mathbf n$, you’re now left with finding a rotation that maps it to the $z$-axis, a well-studied problem. (I’d be tempted to cheat and use a reflection instead because that’s much easier and less expensive to construct.) If you need the centers of the rotated cube’s faces, recall that the columns of a transformation matrix are the images of the basis vectors, so the columns of the rotation matrix are the three independent face normals of the rotated cube. They are unit vectors, so multiply them by $\frac12$. Finally, if you fix the rotation axis as $(1,-1,0)^T$, which is parallel to $\mathbf n(A)\times\mathbf k$ and work out the rotation matrix as a function of $A$, you will get something very similar to the final result in AlexanderJ93’s answer.