2

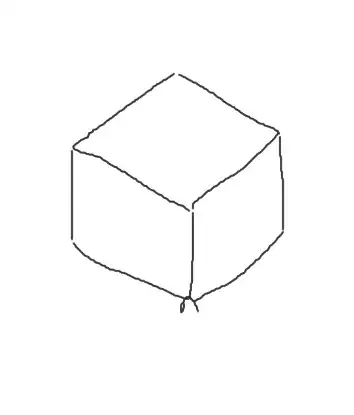
Imagine a cube on a flat table, tantalizingly balanced on one of its vertices such that the vertex most distant from it is vertically above it. What will be the projection on the table if there is a light source right above the cube? What would be the cross-section obtained if we slice the cube along a plane parallel to the table, passing through the midpoint of the topmost and the bottommost points of the cube?

This question is from https://gurmeet.net/puzzles/cube-problems/index.html

My approach: Since the cube would be such that 2 vertices will be exactly above 2 other vertices and topmost vertex is directly above bottommost vertex, thus only 4 vertices will be in the path of light, thus creating a square shadow. However, the answer says a hexagon. I'm not sure why that should be correct.

The way I imagine this cube to be balanced

Charlie
  • 325
  • 4
    Look at the boundary of the figure you have drawn. – Narasimham Aug 10 '23 at 18:41
  • See the anwers in https://math.stackexchange.com/questions/2725780/orthogonal-projection-area-of-a-3-d-cube – GKordas Aug 10 '23 at 19:17
  • 1
    Only one vertex will be directly over another vertex, I do not understand why you thought there would be a second pair. Those two vertices will be above the center of the shadow, while the other 6 vertices are equally distributed about the boundary of the shadow. – Paul Sinclair Aug 11 '23 at 20:57

1 Answers1

0

face parallel to the wall: if one face of the cube is parallel to the wall, the shadow is a square (4 sides).

space diagonal perpendicular to the wall: if the cube is oriented so that a space diagonal is perpendicular to the wall, the shadow is a regular hexagon (6 sides).

other orientations: considering other orientations, the shadow can be a rectangle or other polygons, but none of these have more than 6 sides.

N ROHIT
  • 1