7

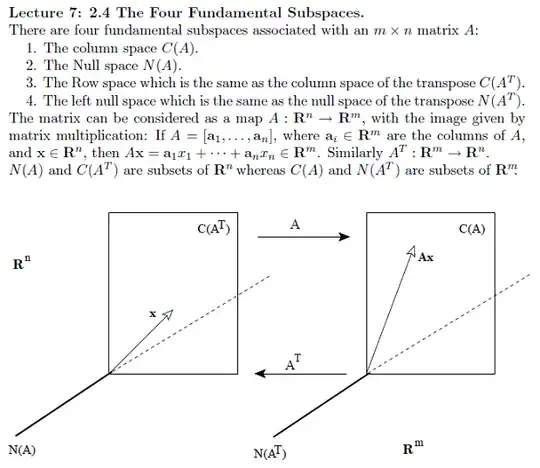
Given a system of linear equations in the form $$AX=b$$ How can I go about visualizing the four fundamental sub-spaces - column space, row space, null space and left null space?

In the same context, how can I visualize the orthogonality of row space and null space, and column space and the left null space?

Chethan Ravindranath
  • 907

1 Answers1

3

I could type it all out, but I think this most efficiently gets you toward what you are after.

enter image description here

Here is the original source.

Here is another way to think about these things from Gilbert Strang:

enter image description here

JohnD
  • 14,681
  • Thanks JohnD! I am still trying to comprehend the first explanation. I am taking the course by Gilbert Strang and have come across the second picture. Hopefully, I will be able to get a clear picture from your answer! – Chethan Ravindranath Jan 09 '13 at 14:52
  • What does the null space of C(A) look like? Is it inside the Columnspace of all Ax? – Learning stats by example Dec 27 '14 at 17:29
  • 1
    @Learningstatsbyexample V old q (& hopefully you found the answer) but, for the record, $\text{c}(A) = \left{c_1\vec{a}_1+c_2\vec{a}_2+\cdots+c_n\vec{a}_n : c_i\in\mathbb{C}\right}$, i.e., it yields a set (containing every possible combination of $A$'s column vectors), NOT a matrix! The 4 fundamental subspaces ($\text{c}(A)$, $\text{c}(A^T)$, $\text{n}(A)$, & $\text{n}(A^T)$) wrt a matrix $A$ yield sets. – Landon Apr 11 '19 at 01:42
  • Makes sense, @Landon. And yeah, my question was 4 yrs ago! – Learning stats by example Apr 11 '19 at 13:15