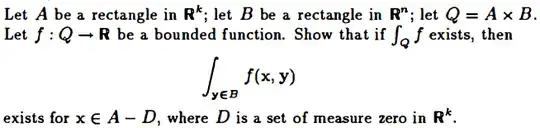Show that if $\int_{Q}f$ exists, then $\int_{y\in B}f(x,y)$ exists for $x\in A-D$, where $D$ is a set of measure zero in $\mathbb{R}^k$

Question

I know that this problem has already been posted here $Q=A\times B$. if $\int_Q f$ exists, then $\int_{y\in B}f(x,y)$ exists for $x\in A-D$, where $D$ is a set of measure zero in $\mathbb{R^k}$. and here if $\int_Q f$ exists then $\int_{y \in B} f(x, y)$ exists for each $x \in A − D$, where $D$ is of measure zero., but the answers do not seem clear to me and a post has no solution. In the second post that I mention, they give a first answer that I do not understand because they use the theory of measure a lot and the truth is that I am a beginner in this and I only have the basic taboo of the measure available, the second answer seems very understandable but unfinished, what else could I do with respect to that second answer? Could anyone help me, please?

Could you help me understand this test that I found? Thank you very much. I do not understand why $f(x)\geq 0$.

Answer 1

In the solution it is better to name $g(x)=\overline{I}(x)-\underline{I}(x)$ insted of $f(x)=\overline{I}(x)-\underline{I}(x),$ since it is confusing with the $f$ of the statement (it is not the same function). Note also that in the solution it is wrong (it says $f(x)=\underline{I}(x)-\overline{I}(x)$ and should be $f(x)=\overline{I}(x)-\underline{I}(x)$). We have $g(x)\geq 0$ for all $x$ by definition of upper and lower integrals (upper integral is always greater than lower integral).

PS: That is Munkres Analysis on Manifolds 13.2 right? You can also use 13.1(b) for this exercise, it is more straightforward.