Lasso ADMM with Positive Constraint

Question

I am solving the Lasso with ADMM.

The problem is given by:

$$ \begin{align*} \arg \min_{x} & \left\{ {\left\| A x - b \right\|}_{2}^{2} + \lambda {\left\| x \right\|}_{1} \right\} \\ \text{ s.t. } & x \succeq 0 \end{align*} $$

I am trying to tackle the inequality constraint by another equality constraint. $$x = \epsilon^2$$

The questions are

Does ADMM support two equality constraint?
Is there another approach to solve Lasso with positive constraint?

Do you mean $ F \geq 0 $ is the constraint you want to add? Are those matrices or vectors? — Royi, Mar 24 '18 at 18:37
OK, This is can be solved in many ways. I will post solution later. — Royi, Mar 25 '18 at 12:26
At this point there are no $F$, $G$, and $M$ in the statement of the question- this seems to have been edited beyond recognition... — Brian Borchers, Mar 25 '18 at 14:10
@BrianBorchers, It was $ M \iff A $, $ F \iff x $ and $ G \iff b $. — Royi, Mar 25 '18 at 18:08
@MarkL.Stone Edited. This is the constraints I was trying to add — Kicr, Mar 27 '18 at 02:09

Royi · Accepted Answer · 2024-06-27T22:34:19.657

This is pretty simple variation of the LASSO as the constraint is easy to solve (Namely its projection has closed form solution which is simple).

Let's define $ f \left( x \right) = \frac{1}{2} \left\| A x - b \right\|_{2}^{2} + \lambda \left\| x \right\|_{1} $.

I solved it using 3 methods.

Projected Sub Gradient Method

The Sub Gradient is given by:

$$ \partial f \left( x \right) = {A}^{T} \left( A x - b \right) + \lambda \operatorname{sign} \left( x \right) $$

The projection onto $ \mathbb{R}_{+} $ is given by:

$$ \operatorname{Proj}_{ \mathbb{R}_{+} } \left( x \right) = \max \left\{ x, 0 \right\} $$

The iteration is simple:

$$ {x}^{k + 1} = \operatorname{Proj}_{ \mathbb{R}_{+} } \left( {x}^{k} - \alpha \partial f \left( x \right) \right) $$

Where $ \alpha $ is the step size of the algorithm.

Proximal Gradient Method

The Proximal Gradient Method for LASSO is well known.
One could see it as a generalization of the Gradient Method.
Hence by adding the Projection Step as above into its iteration solves the problem (Faster) as well.

ADMM

There is a large degree of freedom to solve this using the ADMM Framework.
The approach I did was just a small alteration to the classic solution for the LASSO using ADMM. I just applied the projection on the variable which is being threshold.
It doesn't work perfectly (The Objective Function isn't decreasing monotonically) yet it works really nicely and the idea was from the background of ADMM (Dual Decompositions).

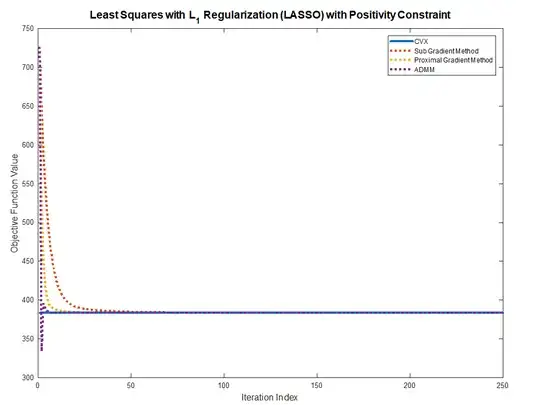
This is the result I got validated against CVX:

Remarks

One could use Accelerated Method to farther speed up the Proximal Gradient Method.
One could formulate the problem using Indicator Function over the non negative orthant. This will yield Classic ADMM for LASSO where the $ x $ iteration will require solving Non Negative Linear Least Squares instead of Linear Least Squares.
There are some other formulations for Constrained LASSO (Though the one above is specific to the above while those are more general) such as:

The code is available at my StackExchange Mathematics 2706108 GitHub Repository.

Nicely explained! what is the CVX and LASS by the way? – Kicr Mar 26 '18 at 01:41 — Kicr, Mar 26 '18 at 01:41

Lasso ADMM with Positive Constraint

1 Answers1

Projected Sub Gradient Method

Proximal Gradient Method

ADMM

Remarks

Linked