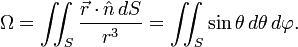0

I am trying to understand this formula from Wikipedia here. It is a generalization of radian. I am trying to do unit check but I cannot see how the units match. Steradion must be dimensioless unit (derived SI unit).

This $\int\int_S \frac{\bar r \cdot \hat n dS}{r^3}$ has area times a small area in the numerator and volume in denomirator so integral of one divided by meter. I am doing somewhere an idea-mistake. Where?

Formula from Wikipedia about solid angle

enter image description here

hhh
  • 5,605
  • The units work out fine! In your last expression using $\theta, \phi$, well, radians are unitless (they're just ratops) as is $\sin \theta$ (which is also just a ratio). Same goes for the first formula -- the dot product leaves a unit in "meters" (for instance) while dS is measured in "meters^2". The reason is that $\vec r$ is a distance vector (meters) while $n$ is a unit vector (with no units). Dividing by the $r^3$ (meters cubed) gives something unitless. –  Jan 04 '13 at 02:41

2 Answers2

1

Think of solid angle as the fraction of a total unit sphere surface area ($4 \pi$) that a cap of the sphere is. The analogy is a fraction of the circumference of a circle that an arc of that circle is, is a circular angle.

Also note that $dS = r^2 \sin{\theta} d \theta d\phi$, and that $\hat{r} . \hat{n} = 1$ for the sphere.

Ron Gordon
  • 141,538
  • Of course, thank you! +1 for the last notice, I had hard time to think the dot product there. For future random walkers, you can find the general case for the area of sphere here with rigorous Jacobian calculations. Have fun! – hhh Jan 04 '13 at 02:18
0

Each vector has its magnitude & direction then we have $$\bar r=|r|\hat r=r\hat r$$ Since, the unit radial vector $\hat r$ & the unit normal vector $\hat n$ to the spherical surface are in the same direction i.e. the angle between these vectors $\alpha=0^{o} \space$ hence we have $$\hat r \cdot \hat n=|\hat r| \cdot |\hat n|cos \alpha=1 \cdot 1 cos0^{o}=1$$ And an elementary area $dS$ on the spherical surface with a radius $r\space$ is given as $$dS=(rd \theta)\cdot(rsin\theta d\phi)=r^2sin\theta d\theta d\phi$$

Where, $\theta$ is angle of longitude & $\phi$ is angle of latitude Now, substituting the corresponding values in left hand side of the expression we get the solid angle $$=\iint_S\frac{\bar r\cdot \hat n \space dS}{r^3}=\iint_S\frac{r(\hat r\cdot \hat n) \space r^2sin\theta d\theta d\phi}{r^3}=\iint_S\frac{r^3(1)\space sin\theta d\theta d\phi}{r^3}=\iint_Ssin\theta d\theta d\phi$$

It is obvious that the solid angle is a dimensionless quantity having SI unit Ste-radian (sr).

Harish Chandra Rajpoot
  • 38,565