1

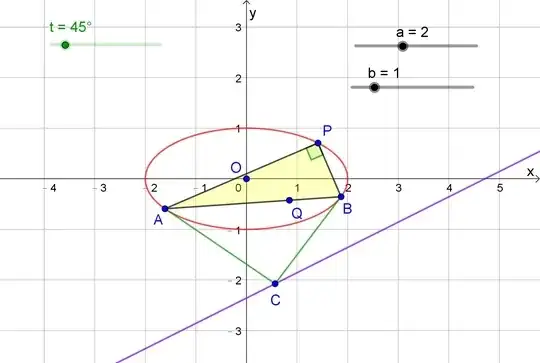
Variable pair of chord at right angle are drawn through point $P$ whose eccentric angle is $45^\circ$ on the ellipse $\frac{x^2}{4}+y^2=1$, to meet the ellipse at $2$ points, say $A$ and $B$. If the line joining $A$ and $B$ passes through a fixed point $Q(a,b)$. Then $a^2+b^2$ is

My trial:

Coordinate of point $P$ is $\left( \sqrt{2},\frac{1}{\sqrt{2}} \right)$.

Now equation of line through $P$ which meets ellipse at $A$ is $y-\frac{1}{\sqrt{2}}=m_{1}(x-\sqrt{2})$

Now equation of line through $P$ which meets ellipse at $B$ is $y-\frac{1}{\sqrt{2}}=m_{2}(x-\sqrt{2})$

And $m_{1}\cdot m_{2}=-1$.

Could some help me to solve it, thanks

Ѕᴀᴀᴅ
  • 35,369
DXT
  • 12,047

2 Answers2

2

Interesting findings without proof

  • Ellipse

    $$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$$

  • $P=(a\cos \theta,b\sin \theta)$

  • $Q=\dfrac{a^2-b^2}{a^2+b^2}(a\cos \theta,-b\sin \theta)$

  • $Q$ is known as Frégier's point

  • $PQ$ is the normal of the ellipse

  • Pole of $AB$ falls on a straight line (point $C$ in the figure below) which is the polar of $Q$

  • In particular, $\theta=\left(n+\dfrac{1}{4} \right) \pi \implies OQ \perp PQ$

  • In this case, $Q=\left( \dfrac{3\sqrt{2}}{5}, -\dfrac{3}{5\sqrt{2}} \right)$ hence $OQ^2=\dfrac{9}{10}$

enter image description here

Ng Chung Tak
  • 19,693
  • My Approach:

    Note:-$m_{AB}$ denotes Slope of $AB$.

    Equation of $AB$ is

    $\frac{y}{1}\cdot sin \frac {(\alpha + \beta)}{2}+ \frac{x}{2}\cdot cos\frac {(\alpha+ \beta)}{2}= cos\frac {(\alpha -\beta)}{2}$

    Let $A=(2cos\alpha,sin\alpha)$ and $B=(2cos\beta,sin\beta)$ $P=(2cos\frac{\pi}{4},sin\frac{\pi}{4})$

    $m_{AP}=\frac{sin\alpha - \frac{1}{\sqrt2}}{{2cos\alpha}-\frac{2}{\sqrt2}}$

    $m_{BP}=\frac{sin\alpha - \frac{1}{\sqrt2}}{{2cos\alpha}-\frac{2}{\sqrt2}}$

    Because $AP$ and $BP$ are perpendicular so $m_{AP}\cdot m_{BP}=-1$

     – mathophile Jun 22 '21 at 09:29
  • After solving I reach to $\frac{5}{2}cos(\alpha-\beta)+\frac{3}{2}cos(\alpha+\beta)$= $\frac{2cos \frac{\alpha- \beta}{2}}{\sqrt2} \biggl ( sin \frac {(\alpha - \beta)}{2}+cos\frac {(\alpha - \beta)}{2}\biggl)+\frac{5}{2}$ – mathophile Jun 22 '21 at 09:29
  • How to processed further? – mathophile Jun 22 '21 at 09:31
0

Since, per the conditions of the problem, all of the lines through the endpoints $A$ and $B$ of the perpendicular chords meet at a common point, you can choose a pair of convenient ones to work with.

Taking the horizontal and vertical chords through $P$ first, by symmetry $A=\left(-\sqrt2,\frac1{\sqrt2}\right)$ and $B=\left(\sqrt2,-\frac1{\sqrt2}\right)$, and the line through them is $x+2y=0$. For the second line, a reasonably convenient choice is the vertical line $x=a$ (with $a$ yet to be determined). The intersection point of these two lines is easily found to be $\left(a,-\frac a2\right)$, from which $a^2+b^2=\frac54 a^2$.

All that’s left to do is to find $a$. This line intersects the ellipse at $\left(a,\pm\frac14\sqrt{16-a^2}\right)$. The condition that the lines through these points and $P$ be perpendicular leads to a quadratic equation in $a$ that I’ll leave for you to derive and solve. One of the solutions to this quadratic equation results in an intersection point outside of the ellipse, which can be rejected. The other gives the required result.

amd
  • 55,082