This question has kind of two parts:
Is it possible to find a closed non recursive form of $f(x)$ where $f(x) = \sin(x + f(x))$.
If the answer to 1 is no, then is it possible to approximate this function in a less computationally expensive way than $f_k(x) = \sin(x + f_{k-1}(x))$
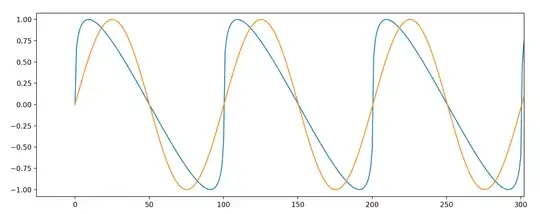
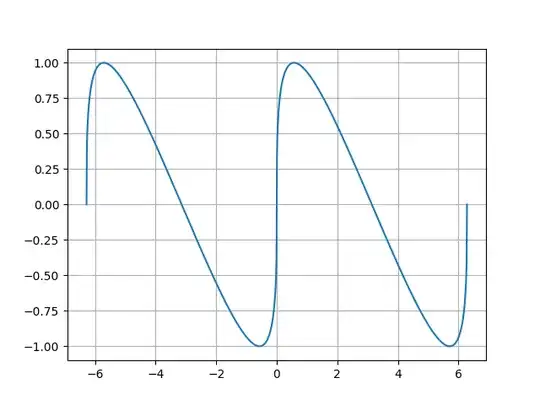
Using the $f_k(x)$ at a depth of $k>10000$ I seem to be able to find that $f_k(x)$ as $k$ approaches ∞ converges to the following graph, where the blue line is $f_{10000}(x)$ and the orange line is $\sin(x)$.
I have tried searching google and here but I can't seem to find any information on what techniques I could use to find a non-recursive form or a better approximation of an infinitely recursive function like $f(x)$.