Probability that two random numbers have a Sørensen-Dice coefficient over a given threshold

Question

The following problem came up at work and my probability knowledge isn't up to the task. Let $a, b \in \mathbb{Z}_{2^n}$ be two $n$ bit integers. Their Sørensen-Dice coefficient is the quantity $$ DS(a, b) = \frac{2|a \wedge b|}{|a| + |b|} $$ where $|a|$ denotes the population count of $a$ (number of 1 bits) and $a\wedge b$ is bitwise AND. I would like to know:

Given $t \in [0, 1]$, what is the probability that $DS(a, b) \ge t$ for $a, b$ drawn uniformly at random from $\mathbb{Z}_{2^n}$?

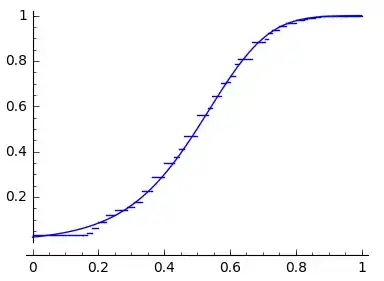
Call this probability $P_n(t)$. Experimentally this probability appears to have the form $$P_n(t) = \frac{1}{1 + 2^{\alpha(t - 1/2)}}$$ where $\alpha$ is some function of $n$. I expect this to be the form of the final answer, albeit with a more precise description of $\alpha$.

Edit: In practice $n$ is 1024 or, more generally, some even power of 512 (I expect the result to hold for general $n$, but maybe that case is easier to handle as a first step).

I would like to be better at solving these kinds of problems, so I will gratefully accept any recommendations for further reading too.

Answer 1

In this question, the Sørensen-Dice coefficient is the ratio $$R_n = \frac {\displaystyle 2\sum_{i=1}^n X_iY_i} {\displaystyle \sum_{i=1}^n X_i + \sum_{i=1}^n Y_i}$$ where all $X_i$ and $Y_i$ are iid $\text{Bernoullli}\left({1\over 2}\right)$. Now the products $X_iY_i$ are iid $\text{Bernoulli}\left({1\over 4}\right)$, so $$R_n={U_n\over V_n},$$ where $$U_n:=2\displaystyle \sum_{i=1}^n X_iY_i\overset{d}{=}2\,\text{Binomial}\left(n,{1\over 4}\right)\overset{d}{\approx} \text{Normal}\left({n\over 2},{3n\over 4}\right)$$ and $$V_n:=\displaystyle \sum_{i=1}^n X_i + \sum_{i=1}^n Y_i\overset{d}{=} \text{Binomial}\left(2n,{1\over 2}\right)\overset{d}{\approx} \text{Normal}\left({n},{n\over 2}\right)$$ and the correlation coefficient is (after some tedious arithmetic) $$\rho(U_n,V_n)={\text{Cov}(U_n,V_n)\over \sqrt{\text{Var}(U_n)\,\text{Var}(V_n)}}=\sqrt{2\over 3}\quad\text{(independent of $n$ !)}.$$ Thus, for large enough $n$, the ratio $R_n$ is approximately distributed like the ratio of two correlated Normal random variables. An approximation due to Hinkley then gives $$P[R_n\le t]\approx \Phi\left({\theta_2 t-\theta_1\over \sigma_1\,\sigma_2\,a(t)}\right)$$ where $\Phi$ is the Standard Normal CDF, and $$\begin{align} \theta_1&=E(U_n)={n\over 2}\\ \theta_2&=E(V_n)=n\\ \sigma_1^2&=Var(U_n)={3n\over 4}\\ \sigma_2^2&=Var(V_n)={n\over 2}\\[2ex] a(t)&=\sqrt{{t^2\over \sigma_1^2}-{2\,\rho\,t\over \sigma_1\sigma_2}+{1\over \sigma_2^2}}=\sqrt{{1\over n}\left({4\over 3}t^2-{8\over 3}t+2\right)}. \end{align}$$ The approximation assumes that $0<{\sigma_2\over\theta_2}\ll 1;$ so, if $n>512$ then ${\sigma_2\over\theta_2}=\sqrt{1\over 2n}\lt 0.04,$ in which case the approximation may be quite acceptable.

---

For small $n$ it's feasible to directly compute the exact distribution of $R_n$ combinatorially, which I've done for $n\le 12$. The following plot for $n=12$ shows the exact CDF of $R_{12}$ (the step function), over which I've superposed Hinkley's approximation (the smooth curve):