8

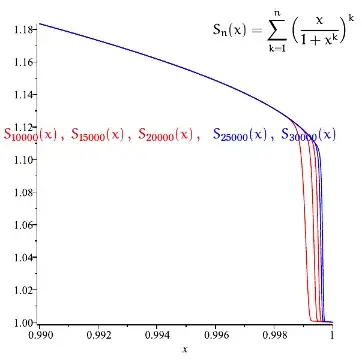
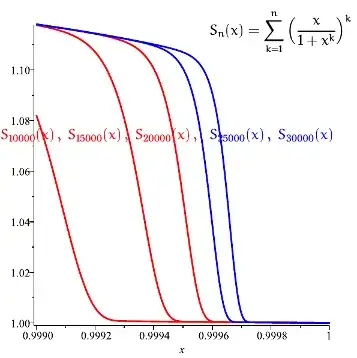
Examine the convergence of the series of functions $$\displaystyle\mathop{\sum}\limits_{n=1}^{+\infty}\Big({\frac{x}{1+x^n}}\Big)^n$$ a) pointwise in $[0,1]$,

b) uniformly in $[0,1]$.

My attempt for pointwise convergence: For all $x\in[0,1)$ exists $n_0(x)\in{\mathbb{N}}$ such that for all $n\in\mathbb{N}$ with $n\geqslant n_0(x)$ : $$\displaystyle\Big|\Big({\frac{x}{1+x^n}}\Big)^n\Big|<\frac{1}{n^2}\,.$$ Because $\sum_{n=1}^{+\infty}\frac{1}{n^2}=\frac{\pi^2}{6}$, we have that the series $\sum_{n=1}^{+\infty}\big({\frac{x}{1+x^n}}\big)^n$ converges pointwise in $[0,1)$. Also for $x=1$ : $\sum_{n=1}^{+\infty}\big({\frac{1}{1+1^n}}\big)^n=\sum_{n=1}^{+\infty}\big({\frac{1}{2}}\big)^n=1$. So, the series converges pointwise in $[0,1]$.

I have no answer for uniform convergence.

edit: This is not an answer for the uniform convergence issue. I'm just giving two plots which shows the behavior of the partial sums sequence $S_n=\sum_{k=1}^{n}\big({\frac{x}{1+x^k}}\big)^k$ near $1$, where is possible the non-uniform convergence of the series $\sum_{n=1}^{+\infty}\big({\frac{x}{1+x^n}}\big)^n$, for helping others to procced further. In the rest of the interval the series looks that converges uniformly. enter image description here

enter image description here

pie
  • 8,483
Grigorios Kostakos
  • 519
  • Hint: Optimze the function $x\mapsto \frac{x}{1+x^{n}}$ on [0,1] – TheOscillator Jan 08 '18 at 20:11
  • @TheOscillator The sequence of functions $f_n(x):=\frac{x}{1+x^n},,; n\in\mathbb{N},,$ does not converges uniformly on $[0,1]$. But how can we use that for the uniform convergence of the series $\sum_{n=1}^{+\infty}\big(f_n(x)\big)^n$ ? There exists a big gap between these two. – Grigorios Kostakos Jan 09 '18 at 13:13
  • That’s interesting ! I don’t see how this question is off topic !! – Tolaso Jan 13 '18 at 15:45
  • 2
    @SangchulLee: This has been asked before here. It is an AMM question from 2000 with a published solution. – RRL Apr 16 '24 at 04:31
  • @RRL, Who, that's good to know, thank you! :) – Sangchul Lee Apr 16 '24 at 05:03
  • @SangchulLee I didn't notice that this is solved in the comment. So why do you still want a bounty? – Liding Yao Apr 23 '24 at 03:05
  • @LidingYao, A bounty can't be cancelled. And it will be still interesting to see any further ideas, because the published solution seems a bit less elegant. I guess it is no harm to give someone credit for spending time and effort to crack down this problem, regardless of whether it is already solved or not :) – Sangchul Lee Apr 23 '24 at 04:24
  • @SangchulLee I see. So what details do you want? I can make it more 'elegant' if I understand what the goal is – Liding Yao Apr 23 '24 at 13:35

2 Answers2

4

This turns out to be a very delicate question because $\max_{0<x<1}(\frac x{1+x^n})^n=\frac1{n-1}(1-\frac1n)^n\sim\frac1{en}$ achieved at $x=(n-1)^{-\frac1n}$. Therefore the divergence test fails but $M$-test also fails.

The answer is that the sum uniformly converges. We need to think of $x\approx2^{-m2^{-m}}$ and consider the sum over $2^{m-1}\le n\le 2^m$.

Let $G\ge100$ and $x_G:=2^{-G2^{-G}}$.

We find the range of $n$ such that $(\frac{x_G}{1+x_G^n})^n\le n^{-2}$, i.e. $n^\frac 2nx_G\le 1+x_G^n$. We claim that it holds when $|n-2^G|\ge 2^G\frac1{\sqrt G}$.

Once the claim is done, then for large enough $M$ \begin{align*} \sup_{0<x<1}\sum_{n\ge M}^\infty\Big(\frac x{1+x^n}\Big)^n\le&\sup_{G>\frac12\log_2M}\sum_{M\le n\le 2^G(1-\frac1{\sqrt G})}\frac1{n^2}+\sum_{|n-2^G|\le 2^G\frac1{\sqrt G}}\frac{100}n+\sum_{n\ge 2^G(1+\frac1{\sqrt G})}\frac1{n^2} \\ \le&\sup_{G>\frac12\log_2M}\frac{200}{\sqrt G}+\frac1M\xrightarrow{M\to\infty}0. \end{align*}

I don't think I have time to check the claim. But by taking derivative with respect to $n$ and plug in $n=2^G(1\pm\frac1{\sqrt G})$ one can see that $n^\frac2nx_G\le 1+x_G^n$ holds.

Liding Yao
  • 3,037
0

Hint:

$$\sqrt[n]{\left(\frac x{1+x^n}\right)^n} =\frac x{1+x^n}\xrightarrow[n\to\infty]{}\begin{cases}x,&x\in[0,1)\\{}\\ \cfrac12,&x=1\end{cases}$$

DonAntonio
  • 214,715
  • Sorry, but I don't understand why this hint tell us something about uniform convergence. – Grigorios Kostakos Jan 08 '18 at 20:44
  • For pointwise convergence: For all $x\in[0,1)$ exists $n_0(x)\in{\mathbb{N}}$, such that for all $n\in{\mathbb{N}}$ with $n\geqslant n_0(x)$ :
    $$\displaystyle\Big|\Big({\frac{x}{1+x^n}}\Big)^n\Big|<\frac{1}{n^2},.$$ Because $\sum_{n=1}^{+\infty}\frac{1}{n^2}=\frac{\pi^2}{6}$, we have that the series $\sum_{n=1}^{+\infty}\big({\frac{x}{1+x^n}}\big)^n$ converges pointwise in $[0,1)$. Also
    $\sum_{n=1}^{+\infty}\big({\frac{1}{1+1^n}}\big)^n=\sum_{n=1}^{+\infty}\big({\frac{1}{2}}\big)^n=1$. So, the series converges point wise in $[0,1]$.     – Grigorios Kostakos Jan 08 '18 at 20:47
  • @GrigoriosKostakos The hint tells you there's pointwise convergence if $;0\le x<1;$ , but divergence if $;x=1;$ ...This already tells you stuff about u.c., doesn't it? – DonAntonio Jan 08 '18 at 22:33
  • No, does not. As stated above the series converges at $x=1$ because $\sum_{n=1}^{+\infty}\big({\frac{1}{1+1^n}}\big)^n=\sum_{n=1}^{+\infty}\big({\frac{1}{2}}\big)^n=1$. Does not diverges. So, uniform convergence remains open. – Grigorios Kostakos Jan 09 '18 at 03:58
  • @GrigoriosKostakos Good point, it is true. Then the OP will still need to make an evaluation as he tried to do from the beginning...and in fact that'll be his answer. – DonAntonio Jan 09 '18 at 08:16