Alternating prime zeta function

Question

Previous question: Alternating prime series

I've been looking at the following function, defined on $\Re(s)>0$.

$$\mathcal P^\star(s)=\sum_{n=1}^\infty\frac{(-1)^{n+1}}{(p_n)^s}$$

where $p_n$ is the $n$th prime.

This function is clearly analytic on $\Re(s)>0$, and so I was curious enough to try and obtain an analytic extension to $s=-1$.

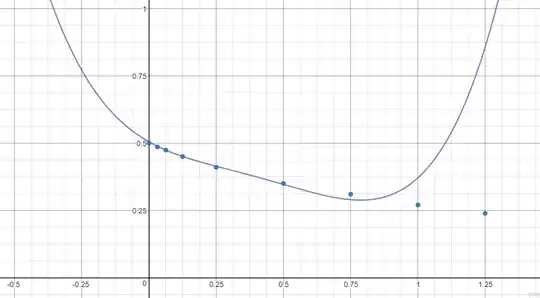
I attempted to compute a few values, and I got the following plot:

And using a linear approximation with the two points closest to $0$, I get

$$\mathcal P^\star(-1)\stackrel?\approx0.95$$

Of course, this is quite naive, and by Taylor exapnding around $0.1$, I got

$$\mathcal P^\star(s)\approx0.459-0.369(s-0.1)+0.690(s-0.1)^2-1.773(s-0.1)^3+1.490(s-0.1)^4$$

The first few Taylor polynomials graphed:

which suggests a pole/singularity at or before $s=-1$.

For comparison, here's the 4th degree Taylor polynomial with the plotted points above:

Can we approximate $\mathcal P^\star(-1)$? And does there exist a singularity for my function in the region $[-1,0)$?

Answer 1

$$\sum_{n=1}^\infty p_{2n-1}^{-s}-p_{2n}^{-s}= \sum_{n=1}^\infty s \int_{p_{2n-1}}^{p_{2n}} t^{-s-1}dt \\=\sum_{n=2}^\infty s\frac{p_{2n}-p_{2n-1}}{p_{2n}^{s+1}}+\mathcal{O}(s^2 n^{-s-2})=s\sum_{n=2}^\infty \frac{g(2n)}{(2n \log n)^{s+1}}+\mathcal{O}(s^2\zeta(\Re(s)+2))$$ Dirichlet series with positive coefficients have a singularity at $s=\sigma$ their abscissa of convergence, here at $s=0$.

Almost everything we can say is conjectural. Under Cramer's model $g(n) $ is a sequence of independent exponential distributions of mean and $\sqrt{}$ variance $\ \ \log n$, thus $\sum_{n \le x} \frac{g(2n)}{\log 2 n} = x + \mathcal{O}(x^{1/2+\epsilon})$ and with $a_s(n) = \log (2n)(2n \log n)^{-s-1}$ $$\sum_{n=2}^\infty \frac{g(2n)}{(2n \log n)^{s+1}} = \sum_{n=2}^\infty (\sum_{m=1}^n \frac{g(2m))}{\log 2m}) (a_s(n)-a_s(n+1))\\=\sum_{n=2}^\infty n\log(2n) (s+1) a_{s+1}(n)+ \mathcal{O}((s+1)n^{-s-2+1/2+\epsilon})$$

and the error term causes many singularities on $\Re(s) = -1/2$.