28

I was curious to know what the following limit is:

$$\lim_{x\downarrow-1}\sum_{n=1}^\infty p_nx^{n-1}=\lim_{x\downarrow-1}(2+3x+5x^2+7x^3+11x^4+\dots)$$

where $p_n$ is the $n$th prime.

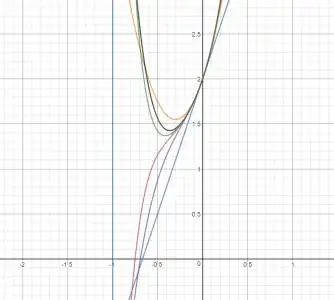
I graphed the first 6 or so partial sums:

enter image description here

but they converge terribly slow. WolframAlpha doesn't seem to have much of a clue either, and with some numerical testing, it seems this limit might go to $\infty$, which is quite strange, since it suggests even and odd indexed primes are not asymptotically equally spaced.

By using some asymptotes on the growth rate of the $n$th prime, one can also easily deduce that

$$\sum_{n=1}^\infty p_nx^{n-1}$$

converges absolutely for $|x|<1$.

Can we prove this limit goes off to $\infty$ or that it exists? And if it does exist, what is it's value?

Simply Beautiful Art
  • 76,603
  • 1
    Here are some computations I've done: taking $x=-1+1/N$ and summing the first $100N$ terms, we get an answer which should be within $10^{-5}$ to the true value, though I didn't do exact estimate): (100, -10.7514398861550) (200, -4.67297770489999) (300, 3.17796306897545) (400, 11.4231942142518) (500, 19.0902610888024) (600, 25.7488008264050) (700, 31.3173570621900) (800, 35.8491110689575) (900, 39.4318049018235) (1000, 42.1548067007355) (1100, 44.1023144294097) Though slowly, it does seem to tend without bound. – Wojowu Dec 26 '17 at 17:32
  • It is quite unlikely that the limit is "something". – Mariano Suárez-Álvarez Dec 26 '17 at 17:37
  • (You did not use "asymptotes on the primes" but "asymptotics on (the growth of) primes". Primes do not have asymptotes) – Mariano Suárez-Álvarez Dec 26 '17 at 17:39
  • 3
    See https://mathoverflow.net/questions/164936/is-the-alternating-sum-of-primes-2-3-5-p-n-asymptotic-to-n-ln-n-2 for something related. – Mariano Suárez-Álvarez Dec 26 '17 at 17:41

1 Answers1

31

Since $p_n=\Theta(n\log n)$ by the weak version of the PNT, we may compute the wanted limit through a convolution with an approximate identity:

$$ \lim_{x\to 0^+} \sum_{n\geq 1}p_n(x-1)^{n-1} = \lim_{n\to +\infty} \sum_{n\geq 1}p_n \int_{0}^{+\infty}n(x-1)^{n-1} e^{-nx}\,dx $$ where $$ \int_{1}^{+\infty}n(x-1)^{n-1}e^{-nx}\,dx = \frac{n!}{e^n n^n}\approx\frac{\sqrt{2\pi n}}{e^{2n}}$$ gives no issues, but $$ \int_{0}^{1}n(x-1)^{n-1} e^{-nx}\,dx=(-1)^{n-1}\int_{0}^{n}\left(1-\frac{x} {n}\right)^{n-1}e^{-x}\,dx $$ behaves like $\frac{(-1)^n}{2}$ for large values of $n$. In particular the existence of the wanted limit depends on the Cesàro summability of the sequence $\{(-1)^n p_n\}_{n\geq 1}$, hence on the distribution of prime gaps.

The result of Ping Ngai Chung and Shiyu Li mentioned on MO implies that the wanted limit does not exist.

Jack D'Aurizio
  • 361,689