1

We roll a die $n = 450$ times to assess whether it is fair, The null hypothesis $H_0$ (that each of the six faces has probability $1/6$ of showing at any one roll) is to be tested at the 5% level of significance.

Let $X_i$ be the number of times face $i$ shows in $450$ rolls. We use the test statistic

$$Q = \sum_{i=1}^6 (X_i -75)^2/75 \stackrel{\text{aprx}}{\sim} \mathsf{Chisq}(\text{df} = 5),$$ rejecting $H_0$ for $Q \ge 11.0705.$

In fact, the die is biased so that the probabilities of the respective faces are truly $p_1 = (1/6, 1/6, 1/9, 2/9, 1/6, 1/6),$ not $p_0 = (1/6, 1/6, 1/6, 1/6, 1/6, 1/6).$

What is the power of the test against this alternative? That is, what is the probability that $H_0$ is (correctly) rejected?

Note: This is not (yet) a homework or examination question. I will post/accept my solution if I do not see an Answer with a better one.

BruceET
  • 52,418
  • $p_1$ is not an admissible set of parameters for the multinomial distribution, since the probabilities do not add to unity. – heropup Nov 23 '17 at 07:17
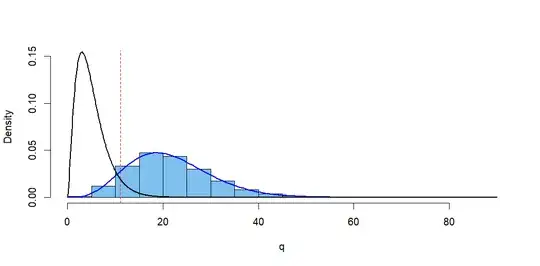
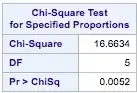
  • @heropup: In R: sum(c(1/6,1/6,1/9,2/9,1/6,1/6)) returns $1.$ Also $1/9 + 2/9 = 1/6 + 1/6 =1/3.$ – BruceET Nov 23 '17 at 07:23
  • Apologies--I commented too hastily, having miscounted. – heropup Nov 23 '17 at 07:24
  • @Heropup: My answer is a generic one that uses a noncentral chi-squared distribution. Maybe for this specific alternative, there is simpler way that I have not found. – BruceET Nov 23 '17 at 07:28
  • Empirically about $0.91$ – Henry Nov 23 '17 at 08:15
  • I was learning about Pearson's Test for Goodness of Fit the other day. Would this be an appropriate method to use to try as an exercise? – Remy Nov 23 '17 at 08:23
  • Maybe by simulation as @Henry did. Certainly, if you know about the noncentral chisquared distribution, and can find the noncentrality parameter. By that method I get power 0.904. – BruceET Nov 23 '17 at 08:27
  • We were examining testing that the true proportions for some groups were .2, .2, .2, .2, .2 but also something like .25, .5, .25 so I might have the required method. – Remy Nov 23 '17 at 08:30
  • @Remy. Then why not give it a try. – BruceET Nov 23 '17 at 08:32
  • @Henry, Here's a rough idea why I posed the question: For certain specific alternatives, you can get way better than 90% power with other approaches. Simple example: Under $H_0,$ the number $X$ of 3's has $P(X \le 62) \approx 0.05,$ but under $H_a: (1/5, 1/5, 0, 1/5, 1/5, 1/5)$ you have power $P(X \le 62) = 1.$ – BruceET Nov 23 '17 at 08:46

2 Answers2

2

If $p_0$ gives the hypothetical probabilities and $p1$ gives the alternative probabilities against which we seek the power then under that $H_a$ we have $Q \stackrel{aprx}{\sim} \mathsf{Chisq}(\nu=5,\lambda),$ where $\lambda = n\sum_{i=1}^6 (p_{1i}-p_{0i})^2/p_{0i} = 16.67$ is the noncentrality parameter.

Then the power $0.904$ can be found using R statistical software as:

lam=16.66667;  1 - pchisq(11.0705, 5, lam) 
## 0.9038942  # power against specified alternative (noncentral chi-sq)

Here is a simulation based on 100,000 repetitions of the 450 roll experiment:

set.seed(1711)
p1 = c(1/6, 1/6, 1/9, 2/9, 1/6, 1/6)
q = replicate( 10^6, chisq.test(table(sample(1:6,450,rep=T,prob=p1)))$stat ) 
mean(q > qchisq(.96, 5))
## 0.89314   # simulate power

The third decimal of the simulation may not be accurate, but also the noncentral chi-squared distribution is itself an approximation, so it's exact value is not guaranteed either.

The figure below shows the histogram of the simulated alternative distribution, which is approximately $\mathsf{Chisq}(5,16.67)$ [blue curve]. The approximate null density function $\mathsf{Chisq}(5)$ [black curve] and the critical value for a test at level 5% [vertical red line] are also shown.

enter image description here

Note: As suggested in one of my Comments, it may be possible to find a test at the 5% level, sensitive to this particular alternative, that gives higher power.

BruceET
  • 52,418
1

I tried using SAS to solve this problem, as that is the program we are learning in my course. This seems like a good exercise for me to try. I am pretty inexperienced with comparing multiple probabilities but this is what I tried.

data gene;
input genotype $ count;
datalines;
A 75
B 75
C 50
D 100
E 75
F 75
;
run;
proc freq data=gene;
weight count;
table genotype / testp=(16.67,16.67,16.67,16.67,16.67,16.65);
run;

enter image description here

What my code is doing is testing the hypothesis that each side has a $1\over6$ chance of happening after obtaining $75$ ones, $75$ twos, $50$ threes, $100$ fours, $75$ fives, and $75$ sixes. In this case we would reject the null hypothesis at $\alpha=0.01$.

However, this is not what the question is asking. How could I adjust my program to find the power of the test?

Remy
  • 8,244
  • Not sure I follow what the SAS code is doing, but this doesn't seem to give the power of the test. But (+1) for giving me something to think about. – BruceET Nov 23 '17 at 08:55
  • Hm, perhaps someone who knows SAS can help me out? – Remy Nov 23 '17 at 08:56
  • Well basically what I tried to do was tell it that we're testing that the probabilities are are $1\over{6}$. That's what the second to last line is doing. And the datelines step is saying that we actually took a sample of $450$ and obtained those numbers which are the each the proportions 1/6, 1/6, 2/9, 1/9, 1/6, and 1/6 you gave. – Remy Nov 23 '17 at 09:09
  • I think the problem is I never tell it what the true proportions are. – Remy Nov 23 '17 at 09:12