Causal inference calculus (Bayesian Probability)

Question

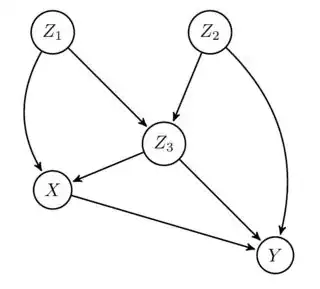
Here is my problem:

There is a causal Markovian model as follows.

By the definition of interventional probability, since $\text{do}(x)$ makes no edges between $X$ and $Z_1, Z_2$, we have

$$ P(y\mid \text{do}(x)) =\sum_{z_1,z_2,z_3}P(z_1)P(z_2)P(z_3\mid z_1, z_2)P(y \mid z_2, z_3, x), > $$ where $\text{do}(\cdot)$ is so-called do-calculus (Judea pearl, 2010).

Then show that the summation over $z_2$ is $$ P(y\mid \text{do}(x)) =\sum_{z_1, z_3} P(z_1) P(z_3\mid z_1)P(y \mid z_1, z_3, x). $$

Here is what is tried.

To hold the equality of the above problem, we must have $$ \sum_{z_2} P(z_3 \mid z_1,z_2)P(y,z_2,z_3,x) $$ should be same with $$ P(y,z_1,z_3,x), $$ but I don't know how this can happen.

Thanks,

Reference: Judea Pearl, 2010, An Introduction to Causal Inference, The International Journal of Biostatistics, pp15-16

Answer 1

I just found that $z_1$ can be inserted in $P(y_1 \mid z_2, z_3, x)$ due to $z_2$ and $z_3$ are sufficient statistics.

$$ P(y_1 \mid z_2, z_3, x) = P(y_1 \mid z_1, z_2, z_3, x) $$

Therefore, the first equation becomes, $$ P(y_1 \mid \text{do}(x)) = \sum_{z_1,z_2,z_3}P(z_1)P(z_2)P(z_3\mid z_1,z_2)P(y_1 \mid z_1, z_2, z_3, x) \\ = \sum_{z_1,z_2,z_3}P(z_1, z_2, z_3)P(y_1 \mid z_1, z_2, z_3, x) \\ = \sum_{z_1,z_2,z_3}P(z_1, z_2, z_3)\frac{P(y_1, z_1, z_2, z_3, x)}{P(z_1, z_2, z_3, x)} \\ = \sum_{z_1,z_2,z_3}P(z_1, z_2, z_3)\frac{P(y_1, z_1, z_2, z_3, x)}{P(z_1, z_2, z_3)} \quad \text{(because X is forced to be constant x)} \\ = \sum_{z_1,z_2,z_3}P(y_1, z_1, z_2, z_3, x) \\ = \sum_{z_1,z_3}P(y_1, z_1, z_3, x) \\ = \sum_{z_1,z_3}P(z_1, z_3) \frac{P(y_1, z_1, z_3, x)}{P(z_1,z_3)} \\ = \sum_{z_1,z_3}P(z_1)P(z_1 \mid z_3)P(y_1\mid z_1, z_3, x) $$