3rd component of a vector from two 2d projections

Question

Let's say I have a particle moving with some velocity $\mathbf{U} = (u,v,w)$, and I can measue a 2D projection of this motion to get $\mathbf{U_{1}} = (u_{1},v_{1})$. One way to estimate the third component would be to image the same particle motion from a different angle.

I then measure $\mathbf{U}$ "from a different plane", rotated by $\alpha, \beta, \gamma \neq N\times90$ about the origin of $\mathbf{U}$ (so both projected vectors have the same origin) and get $\mathbf{U_{2}} = (u_{2},v_{2})$. I know the angles of rotation to align the two planes (and by rotating, say $\mathbf{U_{2}}$ onto the plane of $\mathbf{U_{1}}$ I can get a third component from using the rotation dot product, however, it seems to me that this will only give me a "projected" third component, instead of the "true" component. Writing this question and thinking about it, it's probably not possible to obtain the "real" third component (unless the second measurement was taken at 90 degrees along one axis).

TL;DR

Given an unknown vector $\mathbf{U} = (u,v,w)$, with a known projection $\mathbf{U_{1}} = (u_{1},v_{1})$ in one plane, and another known projection $\mathbf{U_{2}} = (u_{2},v_{2})$ at a different plane rotated around the origin of $\mathbf{U}$ by $\alpha, \beta, \gamma \neq N\times90$ is it possible to obtain $\mathbf{U} = (u,v,w)$?

Potentially similar question, but they wory about scaling and it's only rotation in 2D (I think) How to transform a set of 3D vectors into a 2D plane, from a view point of another 3D vector?

Answer 1

[I’m changing the notation slightly from that in the question. Uppercase symbols represent points/vectors in 3-D, and lowercase points/vectors in 2D.]

This is a fairly straightforward triangulation problem. Let $\mathbf N_1$ and $\mathbf N_2$ be then normals of the planes $\mathbf\pi_1$ and $\mathbf\pi_2$. If $\mathbf U_1$ and $\mathbf U_2$ are the projections of $\mathbf U$ onto these two planes, their back-projections are the lines $\mathbf U_1+\lambda\mathbf N_1$ and $\mathbf U_2+\mu\mathbf N_2$. $\mathbf U$ lies at the intersection of these lines.

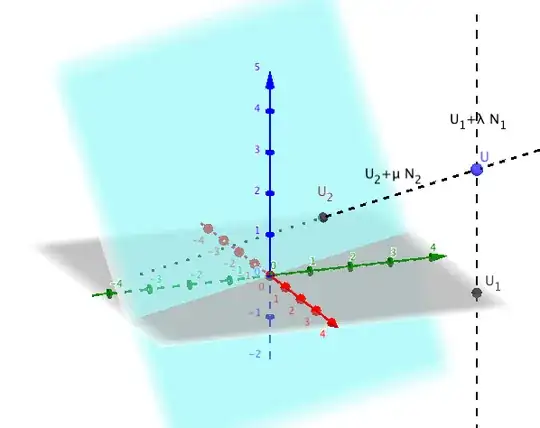
In theory, you just have to compute this intersection to find $\mathbf U$. In practice, for the lines to intersect they must be coplanar and even a small perturbation to $\mathbf U_1$ or $\mathbf U_2$ will destroy this coplanarity. A straightforward way to get an estimate for $\mathbf U$ is to take the midpoint of the points of closest approach of the two lines. You can find a description of this fairly standard computation in this answer by marty cohen and many other places here and elsewhere on the Internet. (Of course, if $\mathbf\pi_1$ and $\mathbf\pi_2$ are two of the coordinate planes, you can just read the coordinates of $\mathbf U$ directly.)

If this estimate isn’t accurate enough, a more sophisticated approach is to find the smallest adjustment (in image space) to $\mathbf U_1$ and $\mathbf U_2$ that makes their back-projections coplanar. This is covered in detail in $§14.4$ of Hartley and Zisserman’s Multiple View Geometry In Computer Vision. I’ll just give the formula here; see the book for full details.

Given the correspondence $(u_1,v_1)\leftrightarrow(u_2,v_2)$ between a pair of points on the respective image planes, we want to find $(\hat u_1,\hat v_1)$ and $(\hat u_2,\hat v_2)$ such that $(u_1-\hat u_1)^2+(v_1-\hat v_1)^2+(u_2-\hat u_2)^2+(v_2-\hat v_2)^2$ is minimized. W.l.o.g. we can take $\mathbf\pi_1$ to be the $u$-$v$ plane, so that its camera matrix is the canonical $$P_1=\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&0&1\end{bmatrix}.$$ This just picks out the $u$- and $v$-coordinates of $\mathbf U$. The projection matrix onto $\mathbf\pi_2$ will have the form $$P_2=\left[\begin{array}{c|c}M_{2\times 3}&\mathbf t\\\mathbf 0^T&1\end{array}\right].$$ The point $\mathbf U$ then satisfies the linear equations $P_1\mathbf U =\mathbf u_1=(u_1,v_1)$ and $P_2\mathbf U = \mathbf u_2=(u_2,v_2)$.

The affine fundamental matrix of this epipolar configuration is $$F_A=\begin{bmatrix}0&0&a\\0&0&b\\c&d&e\end{bmatrix}$$ where $$a = m_{23} \\ b=-m_{13} \\ c=m_{13}m_{21}-m_{11}m_{23} \\ d=m_{13}m_{22}-m_{12}m_{23} \\ e=m_{13}t_2-m_{23}t_1.$$ (In your case, where $P_2$ has no translation component, we would have $e=0$.) The adjusted coordinates are then given by the formula $$\begin{bmatrix}\hat u_2 \\ \hat v_2 \\ \hat u_1 \\ \hat v_1\end{bmatrix} = \begin{bmatrix}u_2 \\ v_2 \\ u_1 \\ v_1\end{bmatrix}-{au_2+bv_2+cu_1+dv_1+e\over a^2+b^2+c^2+d^2}\begin{bmatrix}a\\b\\c\\d\end{bmatrix}.$$ (You might recognize this as the result of a standard least-squares fit, which itself is basically a projection onto a hyperplane in $\mathbb R^4$.) With these adjusted coordinates in hand, you can then find the intersection of their back-projections in the ways described previously.