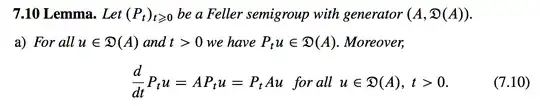14

This is part of a proof to the Feynman-Kac formula from Schilling's Brownian motion. I need some help understanding the proof to this theorem.

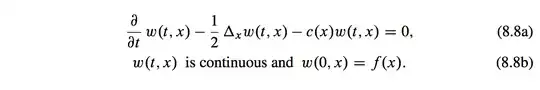
Theorem (Kac 1949). Let $(B_t)_{t\ge 0}$ be a $d$-dimensional Brownian motion, $A$ be the generator of the Feller semigroup $P_t u(x)=E^x u(B_t)$. If $f \in D(A)$ and $c \in C_b (\mathbb{R}^d)$, then the unique solution to the initial value problem (8.8) enter image description here

is given by

$$w(t,x)=E^x \bigg[ f(B_t) \exp \bigg( \int_0^t c(B_r)dr\bigg)\bigg].$$This solution is bounded by $e^{\alpha t}$ where $\alpha=\sup_{x\in \mathbb{R}^d} c(x)$.

Proof. Denote by $P_t$ the Brownian semigroup. Set $C_t := \int_0^t c(B_r)dr$ and $T_t u(x):= E^x (u(B_t)e^{C_t})$. If we can show that $(T_t)_{t\ge 0}$ is a Feller semigroup with generator $Lu=Au+cu$, we are done. Existence follows from Lemma 7.10, uniqueness from the fact that $A$ has a resolvent which is uniquely determined by $T_t$, cf. Proposition 7.13.

Questions. 7.10 is the lemma below and 7.13 states that there is a one-one relationship between the semigroup and the resolvent operator. It seems to me that, to solve this problem, we need to use the uniqueness of the Laplace transform. For instance, below, the author uses it to prove the heat equation Lemma 8.1. However, I cannot directly apply this same method here because $c$ is not a positive constant, so I do not get something of the form $\alpha id - A$, which would be the inverse of the resolvent operator. So, I don't understand how we get uniqueness from Proposition 7.13 as we did in Lemma 8.1 below.

Moreover, I have a question about existence as well. It seems like the author states that existence follows naturally as by Lemma 7.10 we have $\frac{\partial}{\partial t} w(t,x) = Lw$ and $Aw=\frac{1}{2} \Delta w$. However, it is shown in the text that $A= \frac{1}{2} \Delta$ when restricted to $C_\infty^2 (\mathbb{R}^d):=\{u\in C_\infty (\mathbb{R}^d): \partial_j u, \partial_j \partial_k u \in C_\infty (\mathbb{R}^d), j,k=1,\dots ,d\}.$ Also, $C_\infty^2 (\mathbb{R}^d) \subset D(A)$, but is strictly smaller than $D(A)$ for $d>1$. Hence, even if we have $Lu - Au - cu=0$, we cannot guarantee that we have the form $(8.8a)$ where $A= \frac{1}{2} \Delta_x w(t,x)$. So what allows us to conclude the proof here? I would greatly appreciate some help. enter image description here

enter image description here

nomadicmathematician
  • 6,309
  • 1
    Concerning the heat equation and the Feynman-Kac formula, Rene is imprecise (which is very unusual for him). He must certainly be aware of the Tychonoff's example (see e.g. here) of a non-trivial function satisfying the heat equation. The problem is that the proof implicitly assumes that the solution is in the domain of Laplacian. So in order for the theorem to be valid, this should be explicitly written as an assumption (or a class where the equation is considered). – zhoraster Sep 24 '17 at 08:07
  • @zhoraster How about the statement that the uniqueness follows from the fact that $A$ has a resolvent uniquely determined by $T_t$?Even after restricting to the domain of Laplacian, I can't proceed this uniqueness part as in the proof to Lemma 8.1 since $c$ here is not a positive constant but a function. – nomadicmathematician Oct 02 '17 at 13:00
  • Sorry, unfortunately no time at the moment to go deeply into the detail. – zhoraster Oct 02 '17 at 20:07
  • I want to bring up this question again as I do have exactly the same questions. Any ideas so far? – nabla May 28 '19 at 13:00

0 Answers0