22

Question: Find the probability that a random pair of lattice points are opposite corners of a square in an $n\times n$ integer lattice.

Note: By a square in a lattice, I mean a square whose vertices are all lattice points.

Motivation: I have a messy proof that the solution is $\frac13$. The proof relies on calculating the total number of squares in each $n\times n$ lattice, but I want to know if there is some neat argument which avoids that method. There's reason to think there might be since the result is independent of $n$.

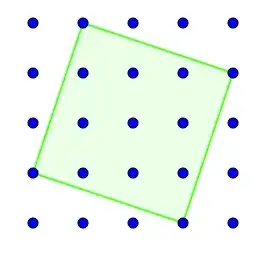
Background: First notice that in an $n\times n$ integer lattice, there are more squares than the obvious axis-aligned squares, for example the following:

squintsquare

With some calculation, one can find that the total number of squares in this grid is $$\sum\limits_{k=1}^nk^2(n-k)=\frac{(n-1)n^2(n+1)}{12}$$ I noticed that this can also be written as $\dfrac{n^2 \choose 2}{6}$, which led me to the combinatorial interpretation of picking corners of a square. Once we know that the number of squares is $\frac{1}{6}$-th of the number of pairs of points, the claimed solution of $\frac13$ is an immediate consequence (as each square has two pairs of opposite corners). However, I've searched for the past week and failed to discover a proof without relying on counting all the squares.

Source: I thought of this question while trying to write problems for a math competition.

Peter Woolfitt
  • 21,476
  • I believe a proof based on induction is well feasible. Given a $n \times n$ square, one considers a $(n+1) \times (n+1)$ square obtained by adding a row and colum of lattice points. It all boils then down to estimating how many diagonals are added, with one point lying in the first square, and the second on the added lattice points. Hopefully, details to be added shortly. – An aedonist Jul 05 '17 at 16:05
  • This is a great problem, but I found your concluding remarks somewhat confusing. What you're saying is that once one knows that the number of squares is $1/6$ times the number of pairs of points, the claim is an immediate consequence (see my now deleted answer also). It might be helpful to state this more explicitly. –  Jul 05 '17 at 20:49
  • You need to better define "opposite corners of a square". I can draw a square with any two points as corners. – user121330 Jul 05 '17 at 20:53
  • 1
    In an infinite grid on the complex plane, that is the set of points $$\Bbb{Z}[i]={a+bi\mid a,b\in\Bbb{Z}}$$ we see that two points, $z_1,z_2$, of the grid are opposite corners of a square of grid points if and only if the components of their difference $$z_1-z_2=a+bi$$ have the same parity (either both odd or both even). This is because then $a+bi$ is divisible by $1+i$ in the ring $\Bbb{Z}[i]$, and the quotient (together with the quotient multiplied by $i$) form the sides of the square. – Jyrki Lahtonen Jul 05 '17 at 21:28
  • 2
    (cont'd) This would suggest that the answer would be $1/2$ if we didn't have to worry about the other two corners falling outside the finite $n\times n$ grid. May be there is a geometric argument for checking how often that happens? I need to get some shut-eye next. Fun problem! – Jyrki Lahtonen Jul 05 '17 at 21:30
  • @user121330 Sorry, I meant they are opposite corners of a square whose vertices are all on the grid. I have added a note to make that clearer. – Peter Woolfitt Jul 05 '17 at 23:16
  • @ChristianRemling Right, I'm sorry it was unclear. I added a sentence to make it better. – Peter Woolfitt Jul 05 '17 at 23:23
  • @PeterWoolfitt: The sequence of the number of squares is archived in OEIS/A002415. – Markus Scheuer Jul 06 '17 at 16:58

3 Answers3

5

For given $k$, $1\leq k\leq n-1$, an axis-aligned square of side length $n-k$ can be placed in $k^2$ ways, and each such square hosts $n-k$ squares with vertices on its rim. The total number $Q_n$ of admissible squares therefore is given by $$Q_n=\sum_{k=1}^{n-1}k^2(n-k)=\ldots={n^2(n^2-1)\over12}\ .$$ I think the exact form of the final result is a coincidence, cf. the formula for $\sum_{k=1}^n k^3$. – Working with the individual choices is made more difficult by the following fact: The chosen points have to fulfill a parity condition before you even can think of a possible square. If $n$ is odd the probability that this parity condition holds is $\ne{1\over2}$.

By the way: Say "a random pair of lattice points" since two points chosen independently can coincide.

Christian Blatter
  • 232,144
1

I think what you outline looks like a fairly optimal (and elegant) solution. As you pointed out, once we have the count of squares inside the grid, the claim is an immediate consequence, by counting in two ways the number of triples $(x,y,Q)$, where $[x,y]$ is a pair of points and $Q$ is a square, and $xy$ is a diagonal of $Q$.

The formula $6(\# Q) ={n^2\choose 2}$ also has a simple proof: We count separately the number of squares that have $(p,q)$ as their bottom edge, with $p\ge 1$, $q\ge 0$. Since this fits into a square of side length $p+q$ with sides parallel to the axes (and this is the smallest such square), we have $(n-p-q)^2$ such squares. This gives $$ \# Q = \sum_{p\ge 1, q\ge 0} (n-p-q)^2 = \sum_{j=1}^n\sum_{p+q=j} (n-j)^2 = \sum_{j=1}^n j(n-j)^2 = \sum_{k=0}^{n-1} k^2(n-k) , $$ as claimed.

While this answer probably just reproduces what you already did yourself, I don't think it's realistic too expect an alternative solution that's much simpler still.

0

Maybe I have an alternative too.

First, one notes that given a $n \times n$ lattice, there are $n- 1 $ ways to draw a square within it. Each square contributes two diagonals. So, the number of diagonals $p(n)$ in a $n \times n$ lattice can be recursively computed as follows: $$ p(n) = p(n-1) + \sum_{k=1}^{n-1} 2k (2n – 2k -1) $$ This is obtained by considering a $n-1 \times n-1$ lattice, and adding points to, say, the bottom and the right side.

One then simply counts, on top of all the diagonals of the initial $n-1 \times n-1$ lattice (first term), the diagonals contained in the squares sharing at least a side with the lines given by the added points at the bottom and the right side. Over-counting is avoided by counting only the diagonals related to lines touching the perimeter of each so defined square, which is done with the formula reported at the beginning. Given a $n \times n$ lattice, the total number of lines $c(n)$ connecting two points is given by $$ c(n) = \frac{n^2 (n^2-1)}{2}$$ For the type of skilled individuals crowding this site (to which I fail to belong), a proof that $$ \frac {p(n)}{c(n)} = 1/3$$ could well be a breeze, using the type of binomial identities the OP suggested.

An aedonist
  • 2,435