1

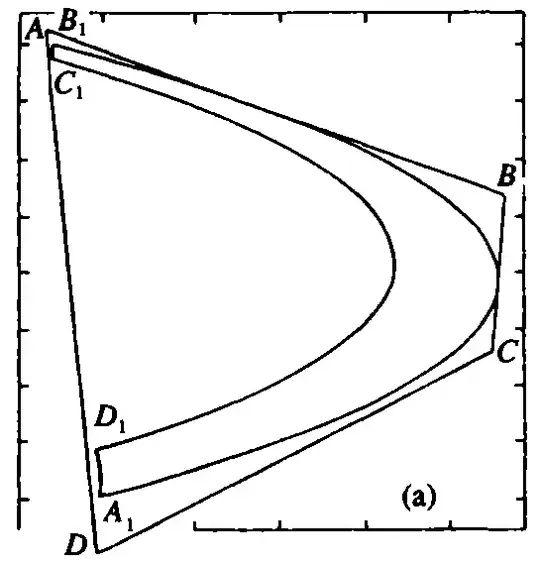
This is probably a relatively straight-forward question but I haven't been to source for a simple enough to understand illustration of a trapping region and bounded trapping region.

Definition:

A trapping region of any dynamic system is a region such that every trajectory that begins in the trapping region will eventually remain in the region's interior for all forward time $t\geq 0$. Trapping region Wiki

Would someone kindly provide an easy to understand illustration?

Did
  • 284,245
Mathematicing
  • 6,541
  • Your question should provide definitions for "trapping region" and "bounded trapping region". – Lee Mosher Jun 12 '17 at 06:07
  • If you are into phase space illustrations of concept, take a look at picture there. Just remove two equilibria at the border and put vectors that point to the inside of the domain instead. – Evgeny Jun 12 '17 at 15:36

2 Answers2

3

Without having seen the definition, a bounded trapping region is probably just a trapping region which is bounded. As for a simple illustration, take the system of a ball rolling on uneven ground. The ball will obviously tend to roll downhill. If there is a hole or a ditch, or anything else vaguely bowl-shaped in the ground, and the ball starts within, then it will never roll out of that hole, which makes the hole a trapping region.

Arthur
  • 204,511
0

A concrete example is given by Hénon in his famous paper A two-dimensional mapping with strange attractor. The quadrilateral $Q=ABCD$ is mapped to the curvilinear quadrilateral $A_1B_1C_1D_1$ which is totally contained in $Q$. Therefore, all orbits of the Hénon map starting in $Q$ remain in $Q$. Hénon gives explicit coordinates for the points $A,B,C,D$.

enter image description here

(Picture from the book "Chaotic evolution and strange attractors" by Ruelle)

lhf
  • 221,500