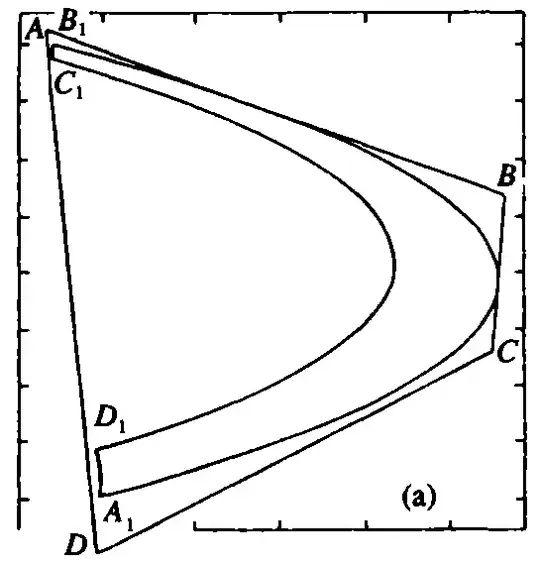
In his famous paper A two-dimensional mapping with strange attractor, Hénon gives an explicit trapping region for the Hénon map with $a=1.3$ and $b=0.4$.
In the figure below, the quadrilateral $Q=ABCD$ is mapped to the curvilinear quadrilateral $A_1B_1C_1D_1$ which is totally contained in $Q$. Therefore, all orbits of the Hénon map starting in $Q$ remain in $Q$. It is in this sense that $Q$ is a trapping region for the map. Hénon gives explicit coordinates for the points $A,B,C,D$.
How did Hénon find the quadrilateral $Q$ explicitly?
How does one find an explicit trapping region for other values of the map parameters $a$ and $b$?
Are there any other large quadrilaterals or triangles that are trapping regions for the Hénon map?
(Picture from the book "Chaotic evolution and strange attractors" by Ruelle)