OP's integral $(3)$ is a good start for contour integration since $\dfrac{ac}b>0$, although the integrand's denominator has an extra term (no $-2ab$). For $t>0$, let
$$I(t) := \int_0^\infty \frac{\arctan u}{\sqrt u\,(u+t)} \, du$$
so that
$$f(a,b,c) = \int_0^\tfrac\pi2 \frac{\arctan\left(a \tan^2x\right)}{b\sin^2x + c\cos^2x} \, dx \stackrel{u=a\tan^2x}= \frac{\sqrt a}{2b} I\left(\frac{ac}b\right)$$
Evaluate $I(t)$ with the residue theorem. Integrate
$$F(z) = \frac{\arctan z}{\sqrt z \, (z+t)} = -\frac i2 \frac{\log \left\lvert\frac{i-z}{i+z}\right\rvert + i \arg\left(\frac{i-z}{i+z}\right)}{\sqrt{\lvert z\rvert} \, e^{\tfrac i2 \arg z} \, (z+t)}$$
along a deformed circular contour avoiding branch cuts along $\pm i [1,\infty)$ and $[0,\infty)$, so that $\arg z\in(0,2\pi)$ and $\arg\left(\dfrac{i-z}{i+z}\right)\in(-\pi,\pi)$. (I'm reusing the image of the contour from one of my older questions; ignore the dotted circles and instead imagine another centered at $z=-\dfrac{ac}b$, anywhere on the negative real axis.)
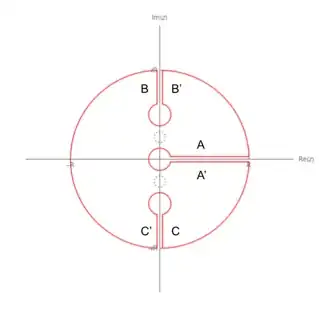
By the residue theorem,
$$\begin{align*}
\oint_\mathcal C F(z) \, dz &= i2\pi \underset{z=-\tfrac{ac}b}{\operatorname{Res}} F(z) = -2\pi \sqrt{\frac b{ac}} \arctan \frac{ac}b
\end{align*}$$
Integrals along the circular components of $\mathcal C$ (small arcs with radius $\varepsilon$ encircling branch points and the large arc of radius $R$) will vanish as $\varepsilon\to0$ and $R\to\infty$. We have $\arg z\to0$ along $A$ and $\to2\pi$ along $A'$, while $\arg\left(\dfrac{i-z}{i+z}\right)\to+\pi$ along $B',C$ and $\to-\pi$ along $B,C'$. The remaining contributions are thus
$$\begin{align*}
\int_A F(z)\,dz &= \int_\varepsilon^R F(x+i\varepsilon) \, dx \to \int_0^\infty \frac{\arctan x}{\sqrt x \, e^{\tfrac i2\cdot0} \, (x+t)} \, dx = I(t) \\
\int_{A'} F &= \int_R^\varepsilon F(x-i\varepsilon) \, dx \to -\int_0^\infty \frac{\arctan x}{\sqrt x \, e^{\tfrac i2 \cdot 2\pi} \, (x+t)} \, dx = I(t) \\
\int_B F &= i \int_{1+\varepsilon}^R F(-\varepsilon+ix) \, dx \to \frac12 \int_1^\infty \frac{\log\frac{x-1}{x+1} - i \pi}{\sqrt x \, e^{\tfrac i2 \cdot \tfrac\pi2} \, (ix+t)} \, dx \\
\int_{B'} F &= i \int_R^{1+\varepsilon} F(\varepsilon+ix) \, dx \to -\frac12 \int_1^\infty \frac{\log\frac{x-1}{x+1} + i \pi}{\sqrt x \, e^{\tfrac i2 \cdot \tfrac\pi2} \, (ix+t)} \, dx \\
\int_C F &= -i \int_{1+\varepsilon}^R F(\varepsilon-ix) \, dx \to -\frac12 \int_1^\infty \frac{\log\frac{x+1}{x-1} + i \pi}{\sqrt x \, e^{\tfrac i2 \cdot \tfrac{3\pi}2} \, (-ix+t)} \, dx \\
\int_{C'} F &= -i \int_R^{1+\varepsilon} F(-\varepsilon-ix) \, dx \to \frac12 \int_1^\infty \frac{\log\frac{x+1}{x-1} - i \pi}{\sqrt x \, e^{\tfrac i2 \cdot \tfrac{3\pi}2} \, (-ix+t)} \, dx
\end{align*}$$
so that upon combining, we have
$$\begin{align*}
-2\pi \sqrt{\frac b{ac}} \arctan \frac{ac}b &= 2 \, I(t) + i\pi \int_1^\infty \left(\frac{e^{i\tfrac\pi4}}{t-ix} - \frac{e^{-i\tfrac\pi4}}{t+ix}\right) \, \frac{dx}{\sqrt x} \\
\implies I(t) &= -\pi \sqrt{\frac b{ac}} \arctan \frac{ac}b + \frac\pi{\sqrt2} \int_1^\infty \frac{x+t}{x^2+t^2} \, \frac{dx}{\sqrt x} \\
&\!\!\!\!\stackrel{x\to\tfrac1{x^2}}= -\pi \sqrt{\frac b{ac}} \arctan \frac{ac}b + \pi\sqrt2 \int_0^1 \frac{1+tx^2}{1+t^2x^4} \, dx \\
&= \frac\pi{\sqrt t} \arctan \frac{\sqrt{2t}}{1-t} - \pi \sqrt{\frac b{ac}} \arctan \frac{ac}b
\end{align*}$$
Now we have
$$I\left(\frac{ac}b\right) = \pi \sqrt{\frac b{ac}} \left(\arctan \frac{\sqrt{2abc}}{b-ac} - \arctan \frac{ac}b\right)$$
and hence
$$\boxed{f(a,b,c) = \frac\pi{2\sqrt{bc}} \arctan \frac{a^2c^2-abc + b\sqrt{2abc}}{b^2-abc+ac\sqrt{2abc}}}$$
where we make use of $\arctan u+\arctan v=\arctan\dfrac{u+v}{1-uv}$. This result agrees with the other answers up to trigonometric identities. JanG's answer, for instance, follows upon recalling $\arctan x=2\arctan\dfrac x{1+\sqrt{1+x^2}}$.
