Imaginary and Complex Dimensions

Question

So I saw a really intriguing question here, and I thought, "Why stop at integers? Why stop at rationals? Why even stop at real numbers?" So I'm asking this: Is there such a thing as imaginary and complex dimensions? Also, on an unrelated note, I wonder what the pith dimension is like. (There probably won't be very much pie there, though.) Also, on another unrelated note, this is my first question. Yay!

Answer 1

One possible answer, based on the work of Michel Lapidus and his collaborators (cited below), is as follows:

Let $A\subseteq \mathbb{R}^N$. For simplicity, suppose that $A$ is bounded (though, it turns out, this hypothesis can be weakened). To $A$, we can associate a distance zeta function, formally defined by the integral $$ \zeta_A(s) := \int_{\{x\in\mathbb{R}^N : d(x,A) < \delta\}} d(x,A)^{s-N}\,\mathrm{d}x, $$ where $\delta > 0$. Note that there is a dependence on $\delta$. However, if $\delta' \ne \delta$, then $$ \int_{\{x\in\mathbb{R}^N : d(x,A) < \delta'\}} d(x,A)^{s-N}\,\mathrm{d}x = \int_{\{x\in\mathbb{R}^N : d(x,A) < \delta\}} d(x,A)^{s-N}\,\mathrm{d}x + h(s), $$ where $h(s)$ is some entire function (i.e. complex analytic on all of $\mathbb{C}$). Ultimately, we are going to be interested in the singularities of $\zeta_A$, so an entire function is irrelevant. In other words, the dependence on a choice of $\delta$ is inessential.

Since $A$ is bounded, the integral will converge whenever $\Re(s) > N$, since the integrand will be bounded above by $|\delta^{s-N}| \le 1$, and the domain of integration will be of finite measure. Indeed, it can be shown that the integral converges for all $s$ with $\Re(s) > \overline{\dim}_B(A)$ and is unbounded at $s=\overline{\dim}_B(A)$, where $\overline{\dim}_B$ denotes the upper-Minkowski dimension. In particular, note that the upper Minkowski dimension of $A$ is a pole of the zeta function.

Now we get to the fun stuff: suppose that $\zeta_A$ can be analytically extended to a function that is meromorphic on a (open) domain that is strictly larger than the half-plane $\{\Re(s) > \overline{\dim}_{B}(A)\}$. In this case, we say that the complex dimensions of $A$ are the poles of this meromorphic extension. It turns out that the set of complex dimensions can give quite a bit of information about the geometry of the set. For example, they give insight into the oscillatory nature of the geometry of a set.

Consider the Cantor set $\mathscr{C}$: it can be shown that the complex dimensions of the usual ternary Cantor set are given by $$ \left\{ \frac{\log(2)}{\log(3)} + i \frac{2\pi k}{\log(3)} : k\in \mathbb{Z} \right\}. $$ That is, there is a periodic set of complex dimensions along the line $\Re(s) = \overline{\dim}_B(\mathscr{C})$, which is telling us that $\delta$-neighborhoods of the Cantor set shrink in an oscillatory manner. These complex dimensions are also related to the spectrum of the Cantor set, in the sense that they describe how a harp consisting of a string in each deleted interval would sound (though the details of this analysis are a bit beyond me).

Short answer: yes, we can define and make sense of a notion of "complex-valued dimensions." This notion can even recover quite a bit of geometric information, which is desirable, as per N.Bach's comment.

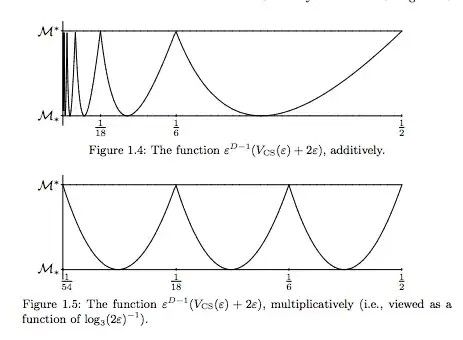
EDITED (to address reuns' comment): The Cantor set is probably the easiest simple motivating example. We can compute the $s$-dimensional upper- and lower-Minkowski contents of the Cantor set by $$ \mathscr{M}^s_{\ast}(\mathscr{C}) = \liminf_{\delta\to 0} \frac{|\mathscr{C}_\delta|}{\delta^{1-s}} \qquad\text{and}\qquad \mathscr{M}^{\ast s}(\mathscr{C}) = \limsup_{\delta\to 0} \frac{|\mathscr{C}_{\delta}|}{\delta^{1-s}}, $$ where $|A|$ is the Lebesgue measure of $A$. The upper and lower-Minkowski dimensions are the smallest values of $s$ for which these values are 0. If it turns out that the two dimensions are both some common value $D$ (as they are in the case of the Cantor set), then we say that the Minkowski dimension is that $D$. We can then ask: What are the $D$-dimensional contents of the set?

If the two contents agree, then we say that the set is Minkowski measurable, with measure equal to its content. In the case of the Cantor set, the contents do not agree, and so the set is not Minkowski measurable. The periodic set of poles over the principle dimension (the dimension at $\log_3(2)$) provide sufficient evidence of this fact. We could also just graph these ratios as a function of $\delta$, which gives something like

(this image is taken from Fractal geometry, complex dimensions and zeta functions, cited below; this is an earlier work that deals mostly with the one-dimensional case).

Note also that the integral looks at $\delta^{N-s}$ (in the case of the Cantor set, $N=1$), though it is thought of as the distance to the set, i.e. the term $d(x,A)^{s-N}$; and integrates over the $\delta$-neighborhood, which plays the role of the measure of the set. Hence it seems reasonable that the distance zeta function should see much of what the Minkowski contents and dimensions see.

Unfortunately, I don't know of an easy explanation for why this is---it requires some theorems (ultimately, I think that you might be interested in are the residue formulae in the two books cited below).

Lapidus, Michel L.; van Frankenhuijsen, Machiel, Fractal geometry, complex dimensions and zeta functions. Geometry and spectra of fractal strings, Springer Monographs in Mathematics. New York, NY: Springer (ISBN 978-1-4614-2175-7/hbk; 978-1-4614-2176-4/ebook). xxvi, 567 p. (2013). ZBL1261.28011.

Lapidus, Michel L.; Radunović, Goran; Žubrinić, Darko, Fractal zeta functions and fractal drums. Higher-dimensional theory of complex dimensions, ZBL06625571.