Suppose $(a,b,c,d)\in \mathbb R^4 $ is nonzero. $ M = \left( {\begin{array}{cc} a & -b & -c &-d \\ b & a & -d & c \\ c &d &a &-b \\ d&-c&b&a \end{array} } \right) $.
Is det$(M)$ non-zero?
Asked
Active
Viewed 289 times
0
-
you sure you have the minus signs correct? – Will Jagy Apr 05 '17 at 18:31
-
@WillJagy Thanks, I edited it. – user136592 Apr 05 '17 at 18:33
-
"$(a,b,c,d)\in \mathbb R^4 $ is nonzero", do you mean different from the zero vector (i.e. not all components 0), or no variable 0 at all? – StackTD Apr 05 '17 at 18:34
-
Still missing a minus in the second row, last column? – StackTD Apr 05 '17 at 18:35
-
@StackTD I mean at least one of the components is nonzero. – user136592 Apr 05 '17 at 18:35
-
1this might follow one of these: https://en.wikipedia.org/wiki/Quaternion#Matrix_representations need to check indicated $i,j,k$ matrices from the question – Will Jagy Apr 05 '17 at 18:37
1 Answers
2
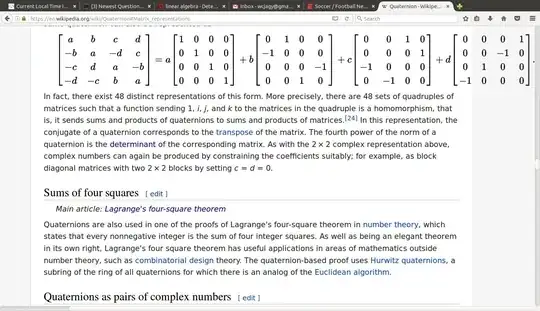
I checked, the way it is typed now agrees with $a (id) + b i + c j + d k$ in https://en.wikipedia.org/wiki/Quaternion#Matrix_representations so the determinant is $$ a^2 + b^2 + c^2 + d^2 $$ and is nonzero if any of the (real) entries is nonzero
The description as SU2, meaning
$$
\left(
\begin{array}{rr}
\alpha & \beta \\
- \bar{\beta} & \bar{\alpha}
\end{array}
\right)
$$
fits with the other (out of 48 possible) set of four matrices on wikipedia,
Will Jagy
- 146,052
-
Is there any way to show that the det agree with its complex form (as an element in SU(2)? – user136592 Apr 05 '17 at 18:44
-
@user, SU2 fits better with a different set of 4 by 4 matrices. Edited in. – Will Jagy Apr 05 '17 at 18:54