As it is discussed here, I got the sense of MPC.
I am confused about which type of solution/cost function or state-space representation to use.
I am trying to implement MPC in MATLAB. I also found some Matlab codes that are different from each other. Thus, I confused again here.
In this reference "Wang, Liuping. Model predictive control system design and implementation using MATLAB®. springer, 2009." there is a part which suggests using some augmented form of the state-space as follow;
$$ \left[\begin{array}{c}\Delta x_m(k+1)\\y(k+1)\end{array}\right]=\left[\begin{array}{c}A_m&o^T_m\\C_mA_m&I_{qx q}\end{array}\right]\left[\begin{array}{c}\Delta x_m(k)\\y(k)\end{array}\right]+\left[\begin{array}{c}B_m\\C_mB_m\end{array}\right]\Delta u(k) $$
$$ y(k)=[o_m I_{qxq}]\left[\begin{array}{c}\Delta x_m(k)\\y(k)\end{array}\right] $$
And the cost function as;
$$ J=(R_s-Y)^T(R_s-Y)+\Delta U^T\bar{R}\Delta U $$
where;
$$
\Delta U=[\Delta u(k_i)^T \Delta u(k_i+1)^T \cdot\cdot\cdot \Delta u(k_i+N_c-1)^T]^T\\
Y=Fx(k_i)+\Phi\Delta U
$$
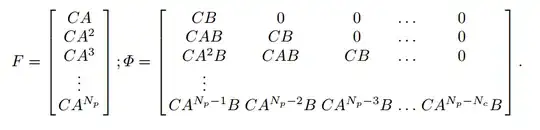
And
Rewriting the cost function and taking derivative with respect to $\Delta U$ to find control inputs which minimize the cost function yields,
$$ \Delta U=(\Phi ^T\Phi+\bar{R})^{-1}\Phi ^T(R_s-Fx(k_i)) $$
in this function when $N_p=20$, $N_c=4$, $A_{m_{3 x 3}}$, $B_{m_{3 x 2}}$, $C_{m_{2 x 3}}$, $\Phi$ becomes 40x8 matrix.
$R_s$ is set-point matrix defined as;
$$ R^T_s=[1 1 \cdot \cdot \cdot 1]_{1xN_p}r(k_i) $$
Parts that I don't understand is here. In the reference, 3 prediction matrices are calculated beforehand as $\Phi^T \Phi, \Phi ^T \bar{R_s}, \Phi ^T F$ where $\bar{R_s}=[1 1 \cdot \cdot \cdot 1]_{1xN_p}$.
The first thing that I don't understand is, why this $\bar{R_s}$ is defined as a vector of 1's. At some point in predicted future, maybe the set-point will not remain constant. Thus, I think the vector should be defined clearly as the set-point($r(k_i)$) values are indicated in the vector.
Second thing is, I couldn't implement this notation to the MIMO case where the number of inputs and outputs are 2 in my case. How should I define the reference matrix when the reference numbers are $y_{ref}=[1\quad2]^T$
I am expecting something like that,
$$ R_s=\left[\begin{array}{cc}0&0\\0&0\\1&2\\1&2\\.&.\\.&.\end{array}\right] $$
But this is a 20x2 matrix where $\Phi^T$ is 8x40 matrix. I know that $R_s$ should be 40x1 but why and how?
By the way, $r(k_i)=[r_1(k_i) r_2(k_i) \cdot \cdot \cdot r_q(k_i)]^T$ for MIMO case.
Edit
Open loop dynamics of the system is; $$ x(k+1)=\left[\begin{array}{c c c}0.6&-0.4&0.2\\1.0&0.4&0.4\\0.8&1.0&0.4\end{array}\right]x(k)+\left[\begin{array}{c c}0.2&0.15\\0.0&-0.5\\0.0&0.05\end{array}\right]u(k)\\ y(k)=\left[\begin{array}{c c c}1.0&-2.2&1.12\\0.0&1.0&1.0\end{array}\right]x(k) $$
And the $\Delta x_m(k)=x(k)-x(k-1)$. Thus state increment related with the control increment $\Delta u(k)$.