1

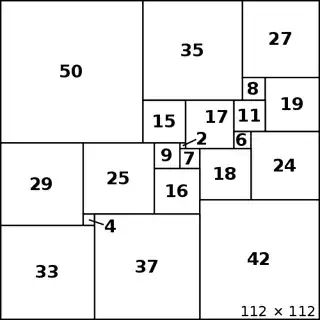
There is a classic problem of 'squaring the square', or constructing a perfect squared square, which is a unit square cut into a finite number of smaller squares whose sidelengths are all different. We know that these sidelengths must be rational so that we need only look for integral tilings; and it turns out solutions do exist to this problem (example shown below). A slightly more general (and much easier) problem which also has solutions is to look for rectangles that can be divided into distinct-sized squares.

A natural generalization is then to look for rectangles which can be tiled by different-sized similar rectangles. Obviously we should ask that our rectangle not be square, but indeed for any perfect squared square, we could simply scale it by an appropriate factor to create a dissection of any rectangle. Thus we could ask that at least one rectangle have a different orientation to the rest, and as far as I can see this makes the problem harder, and I have not found a solution or way of approaching it. It seems interesting to know though which rectangles permit such a tiling.

Thus I have the following question: Is it possible to divide any non-square rectangle into a finite number of rectangles all of different sizes such that all rectangles (including the tiled rectangle) are similar, and such there is a pair of rectangles oriented perpendicularly? If not, which rectangles permit such a dissection? In such a dissection (if one exists), must all of the rectangles be rational scalings of each other?

Lowest-order perfect squared square

$\hskip2in$Squared square

Community
  • 1
Anon
  • 3,363
  • 1
    "different sized congruent rectangles" is a contradiction in terms. If two geometric figures are congruent, then they are the same size. – Gerry Myerson Jan 30 '17 at 08:30
  • 1
    I guess OP meant similar rectangles. I'd guess it should be possible to demonstrate that a $1:\pi$ rectangle doesn't subdivide, but I don't have a specific proof idea, besides perhaps somehow looking at the field extension $\mathbb Q[\pi]/\mathbb Q$ as an infinite-dimensional $\mathbb Q$-vector space. – MvG Jan 30 '17 at 12:19
  • @GerryMyerson I certainly did mean similar. I don't know how that got through. – Anon Jan 30 '17 at 22:23
  • @MvG I wonder if this sort of idea could be used to prove that the sides must be rationally related? – Anon Jan 30 '17 at 22:26
  • 1
    @Anon: Perhaps; it's too late here for me to think this through clearly. During the day I started a draft which might be used to prove that any path along diagonals has to use rectangles of one orientation only. But it's far from clear that one can go from one corner of the big rectangle using only diagonals of the small ones. So one would have to argue about the extra corner coordinates one would introduce even if following a rectangle edge, which complicates matters. – MvG Jan 30 '17 at 22:33
  • @MvG That's an interesting idea. At least such a proof would tell us something, namely that if we follow the diagonals in such a dissection then we get to an edge of the big rectangle, not a corner (unless I'm misunderstanding your comment). Perhaps this would allow us to establish bounds on the number of rectangles used, which might be useful? I'm not really sure. – Anon Jan 30 '17 at 22:38
  • 1
    It might be worth having a look at the paper, Freiling, Laczkovich, and Rinne, Rectangling a rectangle, Discrete Comput. Geom. 17 (1997) 217-225, MR1424825 (97j:52024), and also Prasolov and Skopenkov, Tiling by rectangles and alternating current, J Combin Theory Ser A 118 (2011) 920-937, MR2763046 (2012c:05079). – Gerry Myerson Feb 02 '17 at 02:02
  • @GerryMyerson Those papers look very interesting. I'll take a bit to look through them. – Anon Feb 02 '17 at 04:53
  • At least to me it appears there are two ways to understand your question. Are you looking for any rectangle and a way to tile it in a self-similar fashion? Or are you looking for a way which will be able to generate a self-similar tiling for any rectangle? In the former case, you could pick an aspect ratio to suite your needs, while in the latter case you have to accomodate arbitrary ratios. My comments with $1:\pi$ and so on were aimed at the second interpretation, while the currently accepted example goes for the first. – MvG Feb 02 '17 at 07:00
  • 1
    @MvG I'm wondering which rectangles permit such a tiling. I'd be happy to accept a more general answer. – Anon Feb 02 '17 at 07:05

1 Answers1

2

Here's one example: You can tile an $18\times29$ rectangle with an $18\times9$, an $8\times4$, a $10\times20$, and an $8\times16$. The four tiles are rectangular, similar, of different sizes, with the first two oriented vertically, the other two, horizontally.

EDIT:

It appears that we want the big rectangle similar to the smaller ones. This can be achieved as follows. Let $k=\sqrt{1+\sqrt2}$. Then the four rectangles $(k+2k^3)\times(1+2k^2)$, $(k+k^3)\times(k^2+k^4)$, $k^3\times k^2$, and $k^3\times k^4$ tile a $(k+2k^3)\times(1+3k^2+k^4)$ rectangle. The big rectangle is similar to the others, since the equation $k(k+2k^3)=1+3k^2+k^4$ reduces to $k^4-2k^2-1=0$, or $(k^2-1)^2=2$, which is true.

Gerry Myerson
  • 185,413
  • Thank you for this answer. +1. I realise that I mustn't have written my question clearly enough though, because I actually wanted all of the tiling rectangles to be similar to the big rectangle also. I've edited my question to make it more clear. Thank you for the answer though. – Anon Jan 31 '17 at 02:38
  • I was hoping for a non-trivial extension to squaring the square, where we tile a square with different-sized copies of itself. – Anon Jan 31 '17 at 04:10
  • 1
    You want it, you got it. – Gerry Myerson Jan 31 '17 at 08:17
  • Nice answer! This is interesting. – Anon Feb 01 '17 at 00:20
  • 1
    Thanks for this awesome answer! I just verified the tiling, and I tried to submit an edit with a paint drawing of it but it was rejected. I feel it would improve the answer, though, since it would mean that people wouldn't have to draw the tiling themselves to verify it. Thanks anyway. – Anon Feb 01 '17 at 00:57