0

I am having problems understanding the "intuition", based on vector projections, of the basis transformation matrix:

enter image description here versus the coordinate transformation matrix:

enter image description here as explained on pages 9 and 10 of this Introduction to Tensors online booklet by Kees Dullemond & Kasper Peeter, leading on to the formula:

$$\vec v'= \left(\Lambda^{-1}\right)^\top \vec v$$

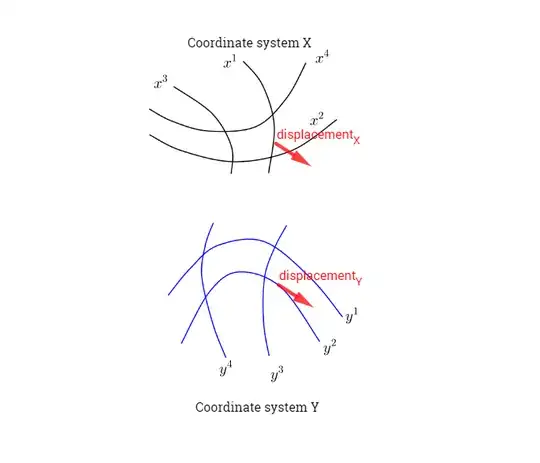
I see the intuition in equation $(2.2)$ looking at the beginning of this youtube video, as applied to the change of coordinates of a differential directional vector from the $X$ coordinate system to the $Y$ coordinate system:

enter image description here

$\begin{align} dY^1 &= \frac{\partial Y^1}{\partial X^1} dX^1 + \frac{\partial Y^1}{\partial X^2} dX^2 + \frac{\partial Y^1}{\partial X^3} dX^3 + \cdots + \frac{\partial Y^1}{\partial X^d} dX^d\\ dY^2 &= \frac{\partial Y^2}{\partial X^1} dX^1 + \frac{\partial Y^2}{\partial X^2} dX^2 + \frac{\partial Y^2}{\partial X^3} dX^3+\cdots+\frac{\partial Y^2}{\partial X^d} dX^d\\ \vdots\\ dY^d &= \frac{\partial Y^d}{\partial X^1} dX^1 + \frac{\partial Y^d}{\partial X^2} dX^2 + \frac{\partial Y^d}{\partial X^3} dX^3+\cdots+\frac{\partial Y^d}{\partial X^d} dX^d \end{align}$

but I still don't see the role or difference with the basis transformation basis (equation 2.1), or the need for the transposition in the $\vec v'= \left(\Lambda^{-1}\right)^\top \vec v.$

Antoni Parellada
  • 10,239
  • The dual nature of basis transformations wrt to coordinate transformation has, indeed, to be considered as an important point in linear algebra. Are you aware of the presentation "alias-alibi" given in the famous book "Algebra" (MacLane and Birkhoff, 1967)? You should find this book in your library. – Jean Marie Jan 25 '17 at 22:54
  • check http://math.stackexchange.com/questions/1667915/change-of-basis/1667996#1667996 for an example of how to think in your case and within an use under a linear transformation – janmarqz Jan 26 '17 at 22:57
  • see also this http://math.stackexchange.com/questions/1005954/how-does-the-representation-of-co-vectors-change-if-we-change-the-basis-of-a-vec/1079587#1079587 – rych Jan 29 '17 at 04:53

0 Answers0