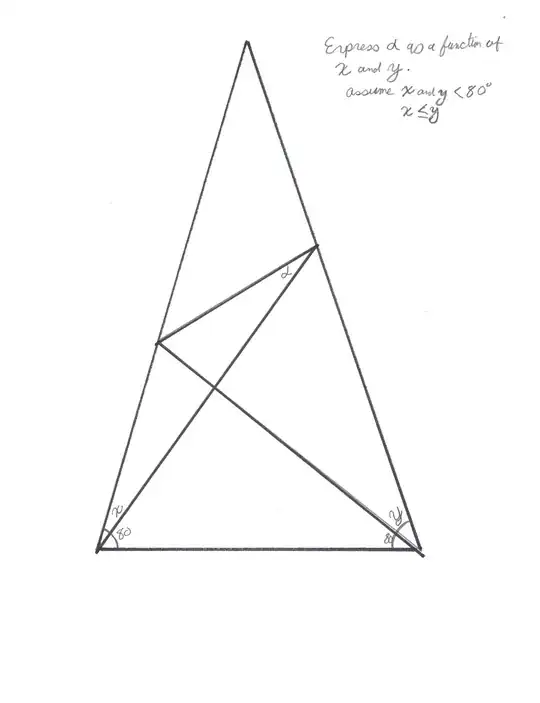
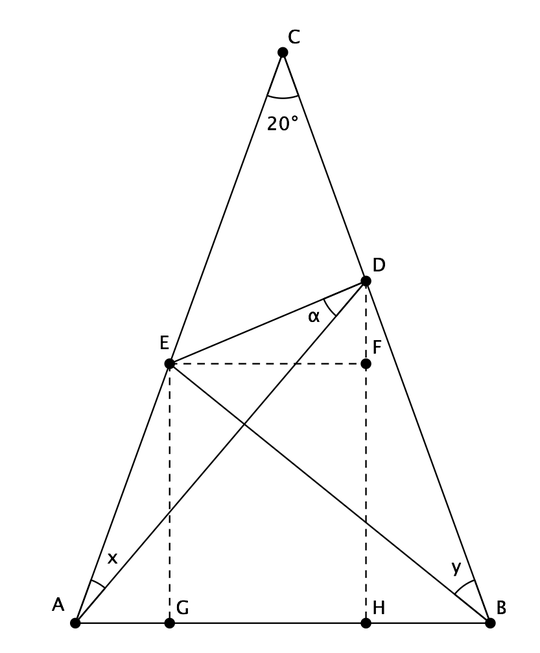
How to express the angle $α$ in terms of $x$ and $y$ when $x$ and $y$ are not known in advance?
One way to approach this is as follows: pick coordinates for the two endpoints of the horizontal line, e.g. $(-1,0)$ and $(1,0)$. Then you can formulate equations for the various lines originating at these points. The lower line on the left for example would be
$$\sin(80°-x)X - \cos(80°-x)Y = -\sin(80°-x)$$
The left hand side is essentially the normal vector of the line. If the line has angle zero against the horizontal, you can imagine the normal pointing down, i.e. $(0,-1)$. For an angle of $90°$ that angle would move from down to right, i.e. $(1,0)$. So we can use $(\sin\varphi,-\cos\varphi)$ here. At the right point, where the angle is measured against the left direction not the right, you'd rather use
$$\sin(80°-y)X + \cos(80°-y)Y = \sin(80°-y)$$
The outer two lines are even simpler:
\begin{align*}
\sin(80°)X - \cos(80°)Y &= -\sin(80°) \\
\sin(80°)X + \cos(80°)Y &= \sin(80°)
\end{align*}
Now you have coordinates for the lines, and can set up systems of equations to obtain the coordinates of the points of intersection. Then you can go about computing the angle $\alpha$ at that one point of intersection. One typical approach would be taking either two difference vectors between points, or two normal vectors of two lines, and then computing the dot product between these. Since the dot product is proportional to the cosine of the angle, you can divide the dot product by the lengths of the vectors, take the arc cosine of that and thus find the angle.
What is it about the nature of this problem that so resists an algebraic solution using similar triangles?
The above works nicely for numeric computations. It also works reasonably well if you know some trigonometric functions of the input angles and want to obtain some trigonometric function of the output ratio. As described above, once you know $\sin$ and $\cos$ of all the input angles, you can compute $\cos^2\alpha$. I'm using $\cos^2$ instead of $\cos$ as you have to divide by the lengths of the two vectors, which involves taking a square root. $\cos^2\alpha$ on the other hand will be a rational function in the trigonometric functions of all the input angles. $\cos\alpha$ will still be some algebraic number.
Now the problem is that while trigonometric functions of a rational number of degrees will be algebraic numbers, the converse is generally not the case. So you have a transcendental relationship between the angle and its cosine, and that's what makes this so difficult to tackle algebraically.
For some specific choices of input angles, these problems lead to a nice integer result, e.g. this one. For others, that is not the case, e.g. this one. Cut the Knot has an overview with some more.