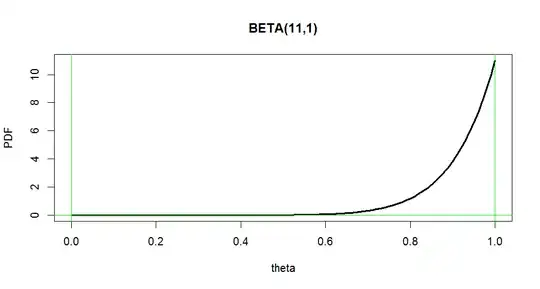
Given some game between two players A and B, after 10 wins of player A and none of player B, how big is the chance of player A to win again? Certainly, one can assume that player A is the more skilled player, since he won all games, but it feels also wrong to assume that player A has a 100% chance of winning now. How can I factor in, that B still has a small chance of winning, and it just didn't occur in that measure? Are there different ways to calculate that?
EDIT To clarify the matter further, I don't look for a calculation that uses a given winning probability for A. Instead I want to understand, what knowledge is included in the fact that I observed 10 wins of A already (e.g. a basketball team won 10 matches against another one). What I can clearly say by this observation is, that A is stronger than B, but I cannot say for sure, that A will win all future games to come.