2

Given two vectors $u = (x_1,y_1)$ and $v=(x_2,y_2)$ there is the dot product $u\cdot v = x_1 x_2 + y_1 y_2$. This has the geometric interpretation $u \cdot v = |u||v|\cos\theta$. The standard proof of that geometric interpretation goes through the law of cosines which itself is proved with the pythagorean theorem or the techniques used in the proof of the pythagorean theorem. For example, the following image illustrates a proof of the law of cosines using the orthocenter. 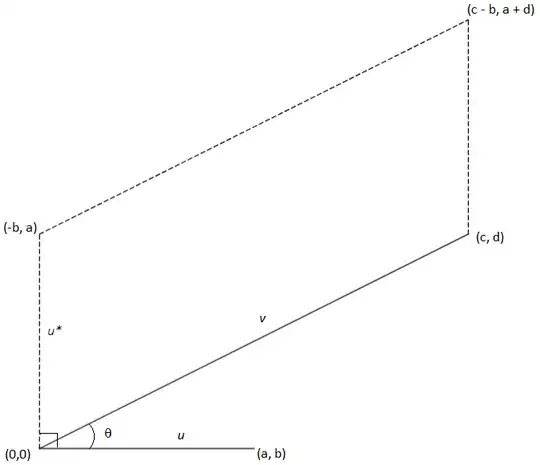enter image description here

But how can one prove $x_1 x_2 + y_1 y_2 = |u||v|\cos\theta$ directly geometrically? There should be some way to prove it using my horribly drawn diagram below. The top left shaded area is $|u||v|\cos\theta$. And the other two shaded areas are $x_1 x_2$ and $y_1 y_2$. How does one prove that using geometry and trigonometry like in the first diagram for the law of cosines.

enter image description here

user782220
  • 3,375
  • How do you define the cosine? My guess is if you get that clearly in your head, the geometric proof will follow. This might give you some yucks: https://arxiv.org/abs/1001.0201 – Charlie Frohman Dec 21 '16 at 20:45
  • So I don't know what proof you intended. But I think I see how to prove it in a way analogous to Euclid's proof of the pythagorean theorem. It requires showing that $|u|(|v|cosθ) = |v|(|u|cosθ)$ in the sense of two rectangles have the same area which requires indroducing trigonometry. The top left area is divided into two parts each corresponding to one of the other areas. A difference is that in Euclid's proof of the pythagorean theorem he in effect showed that in a special scenario without ever introducing trigonometric functions. – user782220 Dec 21 '16 at 22:49
  • 1
    Have you seen the geometric derivation for the angle difference formula $\cos(x-y) = \cos x \cos y - \sin x \sin y$? The dot product is exactly this expression. Hence if you would accept a geometric proof on the angle difference formula, then that is what you want here. – Lee David Chung Lin Oct 08 '18 at 07:31
  • Hey, cool ... That's my diagrammatic proof of the Law of Cosines. See also my Trigonography site. – Blue May 18 '24 at 00:14

1 Answers1

1

After reading the the short post here I wonder if the curiousity about the nature of the equivalence of the geometric and algebraic forms of the dot product arises because the referant has been forgotten: the area of a parallelogram they both describe. Consider three vectors, $u$, $u^*$ and $v$ where $u^*$ is oriented at $90^\circ$ to to $u$, and $v$ cuts the corner at an angle of $\theta$ wrt $u$. enter image description here

We can compute the area of the upper parallelogram geometrically if we consider $u*$ to be the base (with length $|u^*| = |u|$) and note that the width/height is $|v|\cos\theta$: the area is $|u||v|\cos\theta$. We can also compute the area using the algebraic approach in Gauss' area formula. When we let the corner be located at the origin, and the ends of $u$ and $v$ be at $(a,b)$ and $(c,d)$, respectively, then the end of $u^*$ is at $(-b,a)$ and the topmost vertex is at $(c-b,a+d)$. Using these coordinates with Gauss' method computes the area as $ac + bd$ (which is what recognize as the sum of the pairwise products of the coordinate of $u$ and $v$).

So there we have it: since the areas are the same, the expressions must be the same: $u\cdot v = ac + bd = |u||v|\cos\theta$. If the connections between seemingly unrelated things in mathematics is of interest to you, you might enjoy this video which is also discusses the dot product.

smichr
  • 560