How does a disease spread through a triangular network?

Question

Consider a population of nodes arranged in a triangular configuration as shown in the figure below, where each level $k$ has $k$ nodes. Each node, except the ones in the last level, is a parent node to two child nodes. Each node in levels $2$ and below has $1$ parent node if it is at the edge, and $2$ parent nodes otherwise.

The single node in level $1$ is infected (red). With some probability $p_0$, it does not infect either of its child nodes in level $2$. With some probability $p_1$, it infects exactly one of its child nodes, with equal probability. With the remaining probability $p_2=1-p_0-p_1$, it infects both of its child nodes.

Each infected node in level $2$ then acts in a similar manner on its two child nodes in level $3$, and so on down the levels. It makes no difference whether a node is inected by one or two parents nodes - it's still just infected.

The figure below shows one possibility of how the disease may spread up to level $6$.

The question is: what is the expected number of infected nodes at level $k$?

Simulations suggest that this is (at least asymptotically) linear in $k$, i.e.,

$$ \mathbb{E}(\text{number of infected nodes in level } k) = \alpha k $$

where $\alpha = f(p_0, p_1,p_2)$.

---

This question arises out of a practical scenario in some research I'm doing. Unfortunately, the mathematics involved is beyond my current knowledge, so I'm kindly asking for your help. Pointers to relevant references are also appreciated.

I asked a different version of this question some time ago, which did not have the possibility of a node not infecting either of its child nodes. It now turns out that in the system I'm looking at, the probability of this happening is not negligble.

Answer 1

Note: Of course, a most interesting approach would be to derive a generating function describing the probabilities of infected nodes at level $k$ with respect to the probabilities $p_0,p_1$ and $p_2$ and to derive an asymptotic estimation from it.

This seems to be a rather tough job, currently out of reach for me and so this is a much more humble approach trying to obtain at least for small values of $k$ the expectation value $E(k)$ of the number of infected nodes at this level.

Here I give the expectation value $E(k)$ for the number of infected nodes at level $k=1,2$ and propose an algorithm to derive the expectation values for greater values of $k$. Maybe someone with computer based assistance could use it to provide $E(k)$ for some larger values of $k$.

The family of graphs of infected nodes:

We focus at graphs containing infected nodes only which can be derived from one infected root node. The idea is to iteratively find at step $k$ a manageable representation of all graphs of this kind with diameter equal to the level $k$ based upon the graphs from step $k-1$.

Expectation value $E(k=1)$

We encode a left branch by $x$, a right branch by $y$ and a paired branch by $tx+ty$, which is marked with $t$ in order to differentiate it from single branching. No branching at all is encoded by $1$. So, starting from a root node denoted with $1$ we obtain four different graphs: \begin{array}{cccc} 1\qquad&x\qquad&y\qquad&tx+ty\\ p_0\qquad&\frac{1}{2}p_1\qquad&\frac{1}{2}p_1\qquad& p_2 \end{array}

Comment:

• Three of the graphs $x,y,tx+ty$ have diameter equal to $1$ which means they have leaves at level $k=1$.

• These three graphs are of interest for further generations of graphs with higher level.

• Let the polynomial $G(x,y,t)$ represent a graph. The number of terms $x^my^n$ in $G(x,y,t)$ with $m+n=k$ gives the number of nodes at level $k$.

• A node without successor nodes is weighted with $p_0$. We associate the weight $\frac{1}{2}p_1$ to $x$ resp. $y$ if they are not marked and the weight $p_2$ to $tx+ty$.

Description: The first generation of graphs corresponding to $k=1$ is obtained from a root node $1$ by multiplication with $(1|x|y|tx+ty)$ whereby the bar $|$ denotes alternatives. \begin{align*} 1(1|x|y|tx+ty)\qquad\rightarrow\qquad 1,x,y,tx+ty \end{align*}

We obtain \begin{array}{c|c|c} &&\text{nodes at level }\\ \text{graph}&\text{prob}&k=1\\ \hline 1&p_0&0\\ x&\frac{1}{2}p_1&1\\ y&\frac{1}{2}p_1&1\\ tx+ty&p_2&2\\ \end{array}

We conclude \begin{align*} E(1)&=0\cdot p_0 +1\cdot\frac{1}{2}p_1 + 1\cdot\frac{1}{2}p_1+2\cdot p_2\\ &=p_1+2p_2 \end{align*}

$$ $$

Expectation value $E(k=2)$

For the next step $k=2$ we consider all graphs from the step before having diameter equal to $k-1=1$.

These are $x,y,tx+ty$. Each of them generates graphs for the next generation by appending at nodes at level $k$ the subgraphs $1|x|y|tx+ty$. If a graph has $n$ nodes at level $k$ we get $4^n$ graphs to analyze for the next generation.

But, we will see that due to symmetry we can identify graphs and be able to reduce roughly by a factor two the variety of different graphs.

Intermezzo: Symmetry

Note the contribution of graphs which are symmetrical with respect to $x$ and $y$ is the same. They both show the same probability of occurrence.

Instead of considering the three graphs \begin{align*} x,y,tx+ty \end{align*} we can identify $x$ and $y$. We arrange the family $\mathcal{F}_1=\{x,y,tx+ty\}$ of graphs of level $k=1$ in two equivalence classes \begin{align*} [x],[tx+ty] \end{align*} and describe the family more compactly by their equivalence classes together with a multiplication factor giving the number of elements in that class. In order to uniquely describe the different equivalence classes it is convenient to also add the probability of occurrence of a representative in the description. We use a semicolon to separate the probability weight from the polynomial representation of the graph. \begin{align*} \mathcal{[F}_1]=\{2[x;\frac{1}{2}p_1],[tx+ty;p_2]\} \end{align*}

The second generation of graphs corresponding to $k=2$ is obtained from $[\mathcal{F}_1]$ via selecting a representative from each equivalence class and each node at level $k=2$ is multiplied by $(1|x|y|tx+ty)$. The probability of this graph has to be multiplied accordingly with $(p_0|\frac{1}{2}p_1|\frac{1}{2}p_1|p_2)$. We obtain this way $4+4^2=20$ graphs

We calculate from the representative $x$ of $2[x;\frac{1}{2}p_1]$

\begin{align*} x(1|x|y|tx+ty) &\rightarrow (x|x^2|xy|tx^2+txy)\\ \frac{1}{2}p_1\left(p_0\left|\frac{1}{2}p_1\right.\left|\frac{1}{2}p_1\right.\left|\phantom{\frac{1}{2}}p_2\right.\right) &\rightarrow \left(\frac{1}{2}p_0p_1\left|\frac{1}{4}p_1^2\right.\left|\frac{1}{4}p_1^2\right.\left|\frac{1}{2}p_1p_2\right.\right)\\ \end{align*}

We obtain from $2[x;\frac{1}{2}p_1]\in[\mathcal{F}_1]$ the first part of equivalence classes of $[\mathcal{F}_2]$ with multiplicity denoting the number of graphs within an equivalence class. We list the representative and the graphs for each class. \begin{array}{c|l|c|c|l} &&&\text{nodes at}\\ \text{mult}&\text{repr}&\text{prob}&\text{level }2&graphs\\ \hline 2&x&\frac{1}{2}p_0p_1&0&x,y\\ 2&x^2&\frac{1}{4}p_1^2&1&x^2,y^2\\ 2&xy&\frac{1}{4}p_1^2&1&xy,yx\\ 2&tx^2+txy&\frac{1}{2}p_1p_2&2&tx^2+txy,txy+ty^2\tag{1}\\ \end{array}

We calculate from the representative $tx+ty$ of $[tx+ty;p_2]$ using a somewhat informal notation

\begin{align*} tx&(1|x|y|tx+ty)+ty(1|x|y|tx+ty)\\ &\rightarrow (tx|tx^2|txy|t^2x^2+t^2xy)+(ty|tyx|ty^2|t^2xy+t^2y^2)\tag{2}\\ \end{align*}

We arrange the resulting graphs in groups and associate the probabilities accordingly. The graphs are created by adding a left alternative from (2) with a right alternative from (2). The probabilities are the product of $p_2$ from $[tx+ty;p_2]$ and the corresponding probabilities of the left and right selected alternatives.

\begin{array}{ll} tx+ty\qquad&\qquad p_2p_0p_0\\ tx+tyx\qquad&\qquad p_2p_0\frac{1}{2}p_1\\ tx+ty^2\qquad&\qquad p_2p_0\frac{1}{2}p_1\\ tx+t^2xy+t^2y^2\qquad&\qquad p_2p_0p_2\\ \\ tx^2+ty\qquad&\qquad p_2\frac{1}{2}p_1p_0\\ tx^2+tyx\qquad&\qquad p_2\frac{1}{2}p_1\frac{1}{2}p_1\\ tx^2+ty^2\qquad&\qquad p_2\frac{1}{2}p_1\frac{1}{2}p_1\\ tx^2+t^2xy+t^2y^2\qquad&\qquad p_2\frac{1}{2}p_1p_2\\ \\ txy+ty\qquad&\qquad p_2\frac{1}{2}p_1p_0\\ txy+tyx\qquad&\qquad p_2\frac{1}{2}p_1\frac{1}{2}p_1\\ txy+ty^2\qquad&\qquad p_2\frac{1}{2}p_1\frac{1}{2}p_1\\ txy+t^2xy+t^2y^2\qquad&\qquad p_2\frac{1}{2}p_1p_2\\ \\ t^2x^2+t^2y^2+ty\qquad&\qquad p_2p_2p_0\\ t^2x^2+t^2y^2+tyx\qquad&\qquad p_2p_2\frac{1}{2}p_1\\ t^2x^2+t^2y^2+ty^2\qquad&\qquad p_2p_2\frac{1}{2}p_1\\ t^2x^2+t^2y^2+t^2xy+t^2y^2\qquad&\qquad p_2p_2p_2\tag{3}\\ \end{array}

A few words to terms like $txxytyxy$. This term can be replaced with $t^2x^3y^2$. In fact any walk in a graph containing $m$ $x$'s, $n$ $y$'s and $r$ $t$'s (with $t\leq m+n$) can be normalised to \begin{align*} t^rx^my^n \end{align*} If we map this walk to a lattice path in $\mathbb{Z}^2$ with the root at $(0,0)$ and with $x$ moving one step horizontally and $y$ moving one step vertically we always describe a path from $(0,0)$ to $(m,n)$. We could represent each graph as union of lattice paths.

We create now a table as we did in (1). We identify graphs in (3) which belong to the same equivalence class.

\begin{array}{c|l|c|c|l} &&&\text{nodes at}\\ \text{mult}&\text{repr}&\text{prob}&\text{level }2&graphs\\ \hline 1&tx+ty&p_0^2p^2&0&tx+ty\\ 2&tx+txy&\frac{1}{2}p_0p_1p_2&1&tx+txy,txy+ty\\ 2&tx+ty^2&\frac{1}{2}p_0p_1p_2&1&tx+ty^2,tx^2+ty\\ 2&tx+t^2xy+t^2y^2&p_0p_2^2&2&tx+t^2xy+t^2y^2,\\ &&&&t^2x^2+t^2xy+ty\\ 2&tx^2+txy&\frac{1}{4}p_1^2p_2&2&tx^2+txy,txy+ty^2\\ 1&tx^2+ty^2&\frac{1}{4}p_1^2p_2&2&tx^2+ty^2\\ 2&tx^2+t^2xy+t^2y^2&\frac{1}{2}p_1p_2^2&2&tx^2+t^2xy+t^2y^2,\\ &&&&t^2x^2+t^2xy+ty^2\\ 1&2txy&\frac{1}{4}p_1^2p_2&1&txy+txy\\ 2&txy+t^2xy+t^2y^2&\frac{1}{2}p_1p_2^2&3&txy+t^2xy+t^2y^2,\\ &&&&t^2x^2+t^2xy+txy\\ 1&t^2x^2+2t^2xy+t^2y^2&p_2^3&3&t^2x^2+2t^2xy+t^2y^2\tag{4} \end{array}

Combining the classes from (1) and (4) gives $[F_2]$.

We calculate the expectation value $E(2)$ from the tables in (1) and (4) \begin{align*} E(2)&=0\cdot p_0p_1 +1\cdot\frac{1}{2}p_1^2 + 1\cdot\frac{1}{2}p_1^2+2\cdot p_1p_2\\ &\qquad+0\cdot p_0^2p_2+1\cdot p_0p_1p_2+1\cdot p_0p_1p_2+2\cdot 2p_0p_2^2\\ &\qquad+2\cdot\frac{1}{2}p_1^2p_2+2\cdot\frac{1}{4}p_1^2p_2+2\cdot p_1p_2^2+1\cdot\frac{1}{4}p_1^2p_2\\ &\qquad+3\cdot p_1p_2^2+3\cdot p_2^3\\ &=p_1^2+2p_1p_2+2p_0p_1p_2+4p_0p_2^2+\frac{7}{4}p_1^2p_2+5p_1p_2^2+3p_2^3 \end{align*}

Algorithm for $E(k)$

Here is a short summary how $E(k)$ can be derived when $[F_{k-1}]$, the family of equivalence classes of graphs with diameter $k-1$ is already known.

• Take a representative $G(x,y,t)$ from each equivalence class of $[F_{k-1}]$

• Multiply each leave which is at level $k-1$ with $(1|x|y|tx+ty)$

• Multiply the probability of the representative with $(p_0|\frac{1}{2}p_1|\frac{1}{2}p_1|p_2)$ accordingly

• Use $xy$-symmetry of graphs and normalization $t^rx^my^n$ to find new equivalence classes as we did for $k=2$ above. Attention: There may be equivalence classes with equal polynomial representatives but with different probabilities.

• The number of nodes at level $k$ of a graph $G(x,y,t)$ is the number of terms \begin{align*} t^rx^my^n\qquad\qquad m,n\geq 0, 0\leq r\leq m+n=k \end{align*}

• Build $[F_k]$ by collecting all equivalence classes respecting the multiplicity (number of graphs) in an equivalence class

• Calculate $E(k)$

Answer 2

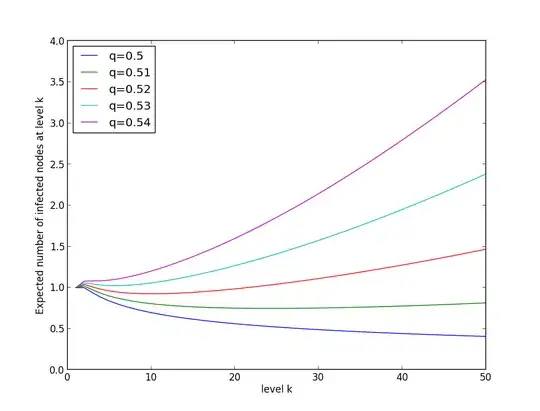
According to discussion in the comments of the question we can conclude that infections of the children of the same node are not independent. But we don't know if that dependence is horizontal or vertical. Meaning, maybe infection of one node has influence on its sibiling, or maybe the parent statistically has higher or lower influence on its children so sometimes it infects both, one or none of them

Since disease spreads vertically only, I will consider the second case

Let parents be named B,L,R or N if they infect both, left, right or none of the children, where $p(L)=p(R)=\frac{p_1}2$. We can draw all possible trees and count their probabilities. For instance $$B$$$$B\_\_R$$$$N\_\_L\_\_R$$$$0\_\_L\_\_0\_\_B$$ $$0\_\_\_1\_\_0\_\_1\_\_\_1$$ has probability $B^3R^2L^2N$ (0-not infected, 1-infected)

Lets discuss all the graphs that end with $01011$, then previous row has to be one of $\{0L0B,R00B,...\}=$ $(\{R\}\times\{0,L,N\}\bigcup \{0,N\}\times\{L\})\times(\{R\}\times\{R\}\bigcup\{0,R,N\}\times\{B\})$

Probability that $01011$ is preceded with $0L0B$ is equal to probability for $0101$ to happen, times $p(L)p(B)$

So $p(01011)=p(1001)p(R)p(B)+p(0101)p(L)p(B) +p(1011)p(R)(p(R)^2+p(R)p(B)+p(N)p(B))+p(0111)p(L)(p(R)^2+p(R)p(B)+p(N)p(B)) +p(1101)(p(R)p(L)+p(N)p(R)+p(N)p(L))p(B) +p(1111)(p(R)p(L)+p(N)p(R)+p(N)p(L))(p(R)^2+p(R)p(B)+p(N)p(B))$

Also $p(1011)=p(1101)$ as a mirror pair

So, it is left to conclude a way of finding preceding combinations for a 011011110... It is made of several groups of consecutive $1$s which are independent, so they can be attached to each other by a Decartes multiplication also multiplied by $\{0,N\}$ for each pair of consecutive $0$s in between.

Let $f(n)$ be the set of all combinations that precede to n consecutive $1$s, $f(1)=\{RN,R0,RL,0L,NL\}$ and lets define $g(n)$ as the set of all elements from $f(n)$ that start with $R$ or $0$ but leading $R$ subtituted with $B$ and leading $0$ subtituted with $L$ , $g(1)=\{BN,B0,BL,LL\}$. Then $f(n+1)=R\times f(n)\bigcup \{R,0,N\}\times g(n)$

Exceptions are the groups on the end or start of the level, where you pick only combinations with leading or ending zero and remove that zero. Lets define sets for leading groups as $lf(n)$, sets for ending groups as $ef(n)$ and groups that are both leading and ending as $lef(n)$

$f(1)=\{RN,R0,RL,0L,NL\}$
$g(1)=\{BN,B0,BL,LL\}$
$lf(1)=\{L\}$, $ef(1)=\{R\}$
$f(2)=\{RRN,RR0,R0L,RNL,RBN,RB0,RBL,RLL,NBN,NB0,NBL,NLL,0BN,0B0,0BL,0LL\}$
$g(2)=\{BRN,BR0,B0L,BNL,BBN,BB0,BBL,BLL,LBN,LB0,LBL,LLL\}$
$lf(2)=\{BN,B0,BL,LL\}$, $ef(2)=\{RR,RB,NB,0B\}$, $lef(2)=\{B\}$
$f(3)=\{RRRN,RRR0,RR0L,RRNL,RRBN,RRB0,RRBL,RRLL,RNBN,RNB0,RNBL,RNLL,R0BN,R0B0,R0BL,R0LL,RBRN,RBR0,RB0L,RBNL,RBBN,RBB0,RBBL,RBLL,RLBN,RLB0,RLBL,RLLL,NBRN,NBR0,NB0L,NBNL,NBBN,NBB0,NBBL,NBLL,NLBN,NLB0,NLBL,NLLL,0BRN,0BR0,0B0L,0BNL,0BBN,0BB0,0BBL,0BLL,0LBN,0LB0,0LBL,0LLL\}$
$lf(3)=\{BRN,BR0,B0L,BNL,BBN,BB0,BBL,BLL,LBN,LB0,LBL,LLL\}$, $ef(3)=\{RRR,RRB,RNB,R0B,RBR,RBB,RLB,NBR,NBB,NLB,0BR,0BB,0LB\}$, $lef(3)=\{BR,BB,LB\}$

Lets calculate p(111),p(110),p(101),p(100),p(010),p(000). With notes that $p(L)=p(10)=\frac {p_1} 2=p(01)=p(R)$, $p(N)=p(00)=p_0$, $p(B)=p(11)=p_2$

$prec(111)=lef(3)=\{BR,BB,LB\}$ is the set of rows that can precede to $111$, so $p(111)=p(11)p(B)(p(B)+p(R)+p(L))$, further I will write just B not p(B)
$prec(110)=lf(2)$,
$p(110)=p(11)(BN+BL+LL)+p(10)B=B(BN+BL+LL+L)$
$prec(101)=lf(1)\times ef(1)=\{LR\}$,
$p(101)=p(11)LR=BLR$
$prec(100)=lf(1)\times \{0,N\}=\{LN,L0\}$,
$p(100)=p(11)LN+p(10)L=BLN+LL$
$prec(010)=f(1)$,
$p(010)=p(11)(RN+RL+NL)+p(10)R+p(01)L=B(RN+RL+NL)+2RL$

$p(000)$ isn't needed and $p(100)=p(001)$, $p(110)=p(011)$

$E(2)=3p(111)+2(p(101)+2p(110))+2p(100)+p(010)= 3p(111)+2p(101)+4p(110)+2p(100)+p(010)= 3p_2^2(p_2+p_1)+2p_2p_1^2/4+4p_2(p_2p_0+p_2p_1/2+p_1^2/4+p_1/2)+p_0p_1p_2+p_1^2/2+p_0p_1p_2+p_2p_1^2/4+p_1^2/2=3p_2^3+5p_2^2p_1+\frac{7}{4}p_1^2p_2+4p_0p_2^2+2p_1p_2+2p_0p_1p_2+p_1^2$

Now you have probabilities on 3rd level you can "easily" calculate them on 4th level

$prec(1111)=lef(4)$
$prec(1110)=lf(3)$,
$prec(1101)=lf(2)\times ef(1)$,
$prec(1100)=lf(2)\times \{0,N\}$,
$prec(1010)=lf(1)\times f(1)$,
$prec(1001)=lf(1)\times \{0,N\}\times ef(1)$,
$prec(0110)=f(2)$,
$prec(1000)=lf(1)\times \{0,N\}\times \{0,N\}$,
$prec(0100)=f(1)\times \{0,N\}$,

Answer 3

We can easily give an asymptotic solution to this problem. Assume the probability that a node in the row $k$ is infected converges to a stable limit $\alpha$ (i.e. it will be the same for each $k\gg1$). Let $x$ be a node in the row $k+1$. Let $$\beta := \frac{1}{2}p_1+p_2,$$ the probability that an infected parent of $x$ infects $x$. If exactly one parent of $x$ is infected, the probability that $x$ is infected is $\beta$, and if both parents are infected, it is $1-(1-\beta)^2 = 2\beta - \beta^2$. Therefore: \begin{align} \alpha =&\ P(x\text{ is infected})\\ =&\ P(\text{exactly one parent of $x$ is infected})\beta\\&+ P(\text{both parents of $x$ are infected})(2\beta-\beta^2)\\ =&\ 2\alpha(1-\alpha)\beta + \alpha^2(2\beta-\beta^2). \end{align} Reordering terms, we obtain the equation $$-\alpha^2\beta^2 + \alpha(2\beta - 1) = 0.$$ This has the solutions $\alpha_1=0$ and $$\alpha_2=\frac{2\beta-1}{\beta^2}.$$ Notice that $\alpha_2\in[0,1]$ if, and only if $\beta\in[\tfrac{1}{2},1]$. This would correspond philosophically to the fact that $\alpha_2$ is a "stable" solution only for $\beta\in[\tfrac{1}{2},1]$, and else $\alpha_1$ is stable.

Can you check to see if you get the same result numerically?

Remark: As remarked in the comments, the probability that a a node in a row is infected depends on the position of the node in the row. The solution I presented ideally approximates the behavior in the middle of the row, where the situation is similar to starting with an infinite row instead of a single node and extending from there.

Answer 4

Interesting problem. I will address the case where each infected node independently infects its two children, each with probability $q$. As discussed in the comments, this is not the same as your stated problem, but since you expressed interest in this problem too, I'll attempt a solution.

My general idea is that if we can find the probability for each node to be infected then we can calculate all other interesting quantities, including the expected value of infected nodes at level $k$.

I started by noticing that a node can be infected via many equal length "paths". The number of paths that exist from the root to any node is a binomial coefficient, and if we were to write the number of all possible paths from root to each node we would end up with Pascal's triangle. I noticed that each of these paths has the same probability to happen, equal to $q^n$, where $n$ is the length of the path. My first thought was that the probability of a node being infected was the number of paths times the probability of a single path. But this is not correct, since the paths are not independent to each other. There is a lot of overlap of the paths, so they are highly dependent. Then I decided to calculate the infection probability recursively, based on the probability of the parents being infected. A node is infected if either parent is infected and it also succesfully transmits the disease to the node of interest, which happens with probability $q$. And conversely, a not is not infected, if none of the parents are infected, or if one or two parents are infected but they do not transmit the disease. Let $P^k_i)$ be the probability of the $i^{th}$ node at level $k$ being infected. Note that the left parent of this node is node $i-1$ at level $k-1$ and the right parent of this node is node $i$ at level $k-1$. Each level $k$, starts with node $1$ and ends with node $k$. If a node does not exist, such as node $0$, or node $k+1$ at level $k$ then we say that it's probability of infection is $0$.

This is how $P^k_i$ is defined recurcively:

$$ \begin{array}{rlr} P^k_i = 1- (&(1-P^{k-1}_{i-1})\cdot(1-P^{k-1}_{i}) \quad &+ \\ & (1-P^{k-1}_{i-1})\cdot P^{k-1}_{i} \cdot (1-q) \quad &+ \\ & P^{k-1}_{i-1}\cdot (1-q) \cdot(1-P^{k-1}_{i}) \quad &+ \\ & P^{k-1}_{i-1}\cdot (1-q) \cdot P^{k-1}_{i}\cdot (1-q) ) \end{array} $$

We can recursively calculate all $P^k_i$ for a large number of levels quickly. Let $N_k$ be the number of infected nodes at level k. The expected number of infected nodes at a level $k$ is simply $$\mathbb E(N_k) = \sum_{i=1}^k P^k_i$$

I wrote a small python program to calculate this for different q. The results are quite interesting. The relationship is not linear with $k$. It looks linear for most values of $q$, but this is just deceptive. Here's a graph of the expected number of infected nodes for $q$ that show the non-linear relationship.

I would like to find a closed form formula for $P^k_i$, but I need to study some background material for this. My current understanding is that since the recursive relationship is not linear, we might not be able to find a closed form.