Division of regular tetrahedron

Question

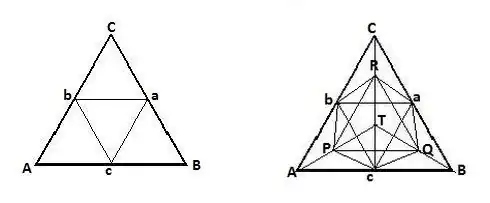
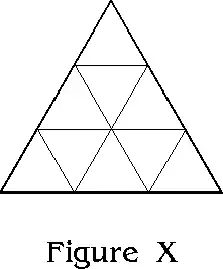
An equilateral triangle can be divided into smaller equilateral triangles by drawing $n$ lines parallel to each side with equal spacing, as this image shows:

_{(source: hermetic.com)}

Moreover, the vertices can be labeled with $1,2,3$ so that each smaller triangle contains exactly one of $1,2,3$. To do this, we start with $1$ on the first row, $2,3$ on the second row, $3,1,2$ on the third row, and so on.

Is there an analogous division and labeling for higher dimensions? For instance, if we start with a regular tetrahedron?

Answer 1

As already pointed out in a comment by Moishe Cohen and especially the comment by Alex Ravsky, the answer is negative. Let attention be restricted to the regular tetrahedron: dividing the length of each edge by two would result in $2^3 = $ eight smaller instances of that regular tetrahedron. Suppose that we try to assemble the original shape with these smaller tetrahedrons, placing four of the $1/8$ ones at the corners of the original to begin with. Then there will be a void in the middle which has the shape of a regular octahedron. It is impossible to fill that void with the remaining four smaller tetrahedrons. I have no rigorous proof for this, but that doesn't serve as a disclaimer. Just use your imagination and you shall see:

The simplified 2-D case is shown in the picture on the left. The picture on the right is the top view of a 3-D wire frame model of the subdivided regular tetrahedron. The four smaller ones at the corners of the original shape ABCT are: AcbP , BacQ , CbaR at the bottom and PQRT at the first floor.

Answer 2

As the perfect division is shall call a division of a regular $d$-dimensional simplex with edge $1$ into $2^d$ its smaller copies with edge $1/2$.

Proposition. The perfect division exists iff $d\le 2$.

Corollary We cannot divide the regular tetrahedron with edge $1$ into $8$ regular tetrahedra with edge $1/2$.

Proof of Proposition. The case $d\le 2$ is clear. Now let $d\ge 3$. A perfect division of a regular $d$-dimensional simplex induces a perfect division of any of its hyperface (that is of the face of dimension $d-1$). By this descent it suffices to show that there is no perfect division $\mathcal D$ for $d=3$, that is of the regular tetrahedron $\Delta$. Indeed, a division $\mathcal D$ induces a division $\mathcal D_F$ of each face $F$ of the tetrahedron into four regular triangles. Let $\Delta_F\in \mathcal D$ be a tetrahedron containing the central triangle of the division $\mathcal D_F$. Let $h_F$ be the height of the tetrahedron $\Delta$ at the face $F$ and $C$ be the center of the tetrahedron $\Delta$. Since the height of the tetrahedron $\Delta_F$ is $|h_F|/2$, and the point $C$ lies at $h_F$ at the distance $|h_F|/4$ from the face $F$, $C$ belongs to the interior of $\Delta_F$. Thus the members of family $\{\Delta_F: F$ is a face of $\Delta\}$ of distinct different tetrahedra of the division $\mathcal D$ overlap at $C$, a contradiction.