Consider an ellipse with semi-axes $a$ and $b$, taller than it is wide with a small circle of radius $r$ inside. Assume the circle falls to the lowest point possible while staying inside the ellipse.
If $2r\le a-c$ then the circle and ellipse will meet at a single point at the bottom. If $2r>a-c$ the circle and ellipse will intersect at two points on the opposite side, leaving a space between the bottom of the circle and the bottom of the ellipse. For this case, given the radius of the circle and the dimensions of the ellipse how do I calculate the distance $d$ between the bottom of the circle and the bottom of the ellipse?
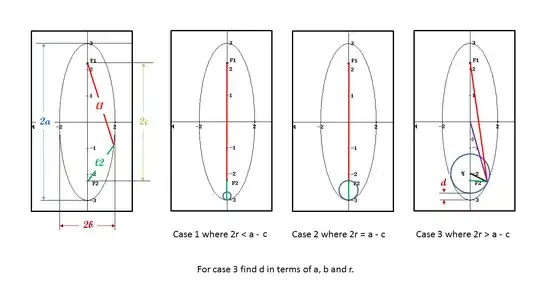
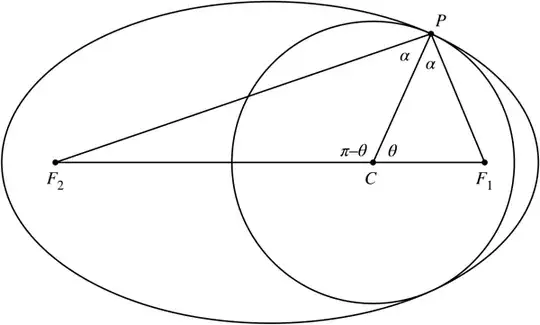
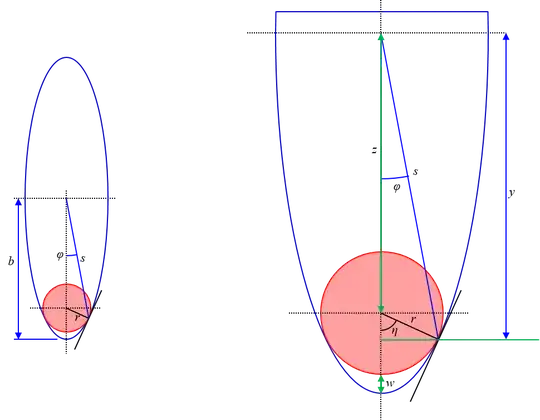
c? The semi-axes areaandband the circle radius isr. Is this correct? – John Alexiou Oct 17 '16 at 18:43