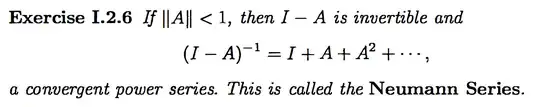On some online forum, there is the claim:
Given some square matrix:
$$(I - A)^{-1} = I + A + A^2 + A^3 + \ldots$$
This is true if the right side converges, which is true if and only if all of the eigenvalues of A have absolute value smaller than $1$.
Reference https://www.physicsforums.com/threads/matrix-inverse-equals-power-series.423897/
I really like this result, because it relies on the more intuitive spectral radius rather than matrix norm which is defined as:
\begin{align} \|A\| &= \sup\{\|Ax\| : x\in K^n \mbox{ with }\|x\|= 1\} \\ &= \sup\left\{\frac{\|Ax\|}{\|x\|} : x\in K^n \mbox{ with }x\ne 0\right\}. \end{align}
Can someone provide a reference to the proof of this claim?