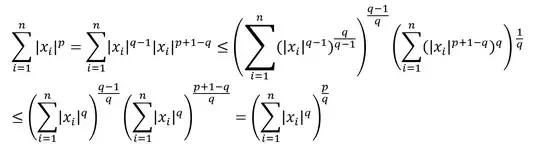Help show $(∑_{i=1}^n |x_i | )^p≥∑_{i=1}^n |x_i |^p $ using common inequalities (like Holder's inequality)

Question

The question is to show

$(∑_{i=1}^n |x_i | )^p≥∑_{i=1}^n |x_i |^p $ for $p\ge1$ , or in plain words, the sum's power is no less than the sum of powers if the power is no less than 1.

It is best that it can be proved using Holder's inequality or any other commonly used inequalities like Minkowski’s inequality. Do not use measure theory (for this is a super-easy special case of Lp norm on counting measure), do not take derivative.

Also do not use the monotonicity of p-norm, because the purpose of this claim is to prove the monotonicity. The above claim is a special case that vector 1-norm is larger than any vector p-norm.

I try to prove this as an effort to prove the monotonicity of p-norm using common inequalities but not taking derivative (see For vector p-norm, can we prove it is decreasing without using derivative?). If the above can be proved, then the monotonicity can be proved by Holder's inequality as the following,

where the second inequality uses above result when moving the power $p+1-q$ outside of the brackets.

Answer 1

More generally, consider $1\leq r\leq p$. Assume $x\neq 0$. From $|x_i|\leq \|x\|_p$ we get that $$1= \sum_i \left( \frac{|x_i|}{\|x\|_p} \right)^p \leq \sum_i \left( \frac{|x_i|}{\|x\|_p} \right)^r = \left( \frac{\|x\|_r}{\|x\|_p}\right)^r$$ from which $\|x\|_p\leq \|x\|_r$. I didn't see a natural way to involve Hölder inequalities in this estimate.

Answer 2

Lets denote by $\|x\|_p$ the $p$-norm of the vector $x$. Set $\theta = 1/p \in [0,1)$. We denote by $|x|^\theta$ the vector with entries $|x_i|^\theta$. Then, you have $$\|x\|_p = \| |x|^\theta \, |x|^{1-\theta} \|_p \le \||x|^\theta\|_{p} \, \||x|^{1-\theta}\|_{\infty} = \|x\|^\theta_1 \, \|x\|^{1-\theta}_\infty \le \|x\|_1. $$ Note that all steps are elementary.