A goat is tied to an external corner of a rectangular shed measuring 4 m by 6 m. If the goat’s rope is 8 m long, what is the total area, in square meters, in which the goat can graze?
Well, it seems like the goat can turn a full circle of radius 8 m, and a rectangular shed's diagonal is less than 8m (actually √52), and so shouldn't it be just 6 x 4 = 24 sq metre? The answer says it is 53 pi, and I have no clue why it is so or why my way of solving doesn't work.
Updated: Oh, and the only area given is that of the shed's. How can I know the full area in which the goat can actually graze on?
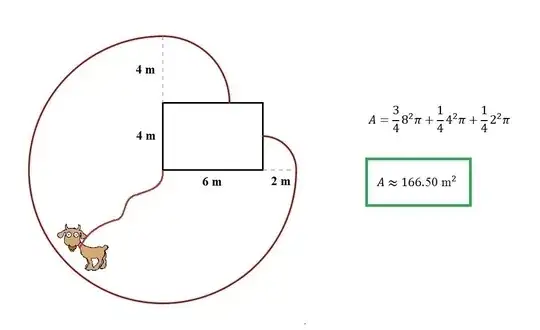
6 x 4that's the area of the shed. The goat grazes outside of the shed, not inside – njzk2 Sep 26 '16 at 16:59