2

I am trying to understand this problem from the movie Good Will Hunting just because it looks fun. It asks to find the generating function for walks from points i to j. I attached a link here http://www.math.harvard.edu/archive/21b_fall_03/goodwill/ that apparently explains it. I am curious how the geometric series holds true for matrices. I am also curious how the matrix A gets thrown into the proof as well. If anyone has any information/resources on how to tackle this problem, I would be very grateful to learn. enter image description here

Math1000
  • 38,041
W. G.
  • 1,856
  • Matt Damon would know... – Michael Sep 26 '16 at 03:33
  • My solution here mostly answers your question: http://math.stackexchange.com/questions/1930609/method-of-generating-function-markov-chain/1930677 – Math1000 Sep 26 '16 at 03:36
  • 2
    If you are looking for the number of walks, it is similar to multiplying transition probability matrices $P$ for discrete time Markov chains to find the $k$-hop transition probabilities $P_{ij}^{(k)}$. Notice: $$\underbrace{(\mbox{num walks $i\rightarrow j$ in $k$ steps})}{A{ij}^{(k)}} = \sum_{n=1}^4\underbrace{(\mbox{num walks $i\rightarrow n$ in $(k-1)$ steps})}{A{in}^{(k-1)}}a_{nj}$$ where $a_{nj}$ is binary indicating if there is a link from $n$ to $j$. – Michael Sep 26 '16 at 03:38
  • 2
    Every answer here really should start with "Do you like apples?", proceed to solve the problem and then end with "How do you like them apples?" – Deepak Sep 26 '16 at 03:48
  • I really do like the comments about the movie:) – W. G. Sep 27 '16 at 17:12

1 Answers1

1

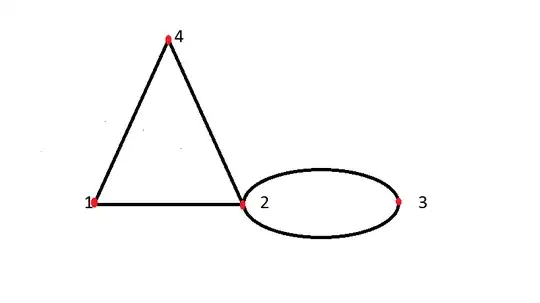
The adjacency matrix counts the number of connections between the various nodes, in the $ij$ increasing fashion. If there is a connection, increase the corresponding count in the matrix by one. For example, in the first row in the matrix (with the nodes labeled as in the picture provided) we would have $[0,1,0,1]$, because node 1 is connected to node 2 and 4, but not connected to node 1 (itself) and node 3. The relation between the adjacency matrix and the solution is the generating function, described in your link.

The geometric series for the matrix is proved in a similar fashion to the normal geometric series. You just have to determine where the series converges. If you are interested, you can find a proof here http://www.math.uvic.ca/~dcwatson/work/geometric.pdf

MarsOneRover
  • 490
  • One caveat is that an adjacency matrix $A$ can have eigenvalues $>1$, so the power series $\sum_{n=0}^\infty (zA)^n$ need not converge for any $z\ne 0$. So we must treat this object as a formal power series instead. – Math1000 Sep 26 '16 at 03:41
  • Using your link I am stuck on one part. I am trying to see where all the zs come into play. Currently I have something like this where Sn=(I-L)^(-1). Can you help me with this part? – W. G. Sep 27 '16 at 17:11
  • I figured it out. z is just a scalar. Good link. – W. G. Sep 28 '16 at 03:14